chap 2-3 分治算法-多项式与快速傅里叶变换

1. 信号处理

在数字信号处理（Digital Signal Processing）领域中，经常使用到多项式乘法。信号通常是一个关于时间或位置的函数，比如捕获到的人的声音等等。数字信号处理要做的事情一般是，先对信号进行采样（sampling），使之变为离散信号；然后将离散信号输入到一个系统中（滤波器等等），最后得到系统的输出，我们称之为系统的响应（response）。

假设现在输入信号为$a(t)$，我们首先使用单位冲激（unit impulse）函数$\delta(t)$对$a(t)$进行采样：

$$
\begin{equation}
\delta(t)=
\begin{cases}
1, & t=0 \\ 0, & t\neq 0
\end{cases}
\end{equation}
$$

若采样点数为$T$（为简化，暂且忽略采样间隔、归一化等细节），则对$a(t)$的采样为：

$$
a(t)=\sum_{i=0}^{T-1}a(i)\delta(t-i)
$$

下一步应该将离散信号输入到系统中，但是如何描述系统本身的性质？若把$\delta(t)$输入到系统中，会得到系统对于单位冲激信号的响应$b(t)$，我们称之为该系统的冲激响应（impulse response）。若系统是线性时不变的（linear and time-invariant），则$b(t)$可以描述该系统的性质；把$a(t)$输入系统，根据上述表达式可知，系统对于$a(t)$的响应完全取决于系统的冲激响应，因此在时刻$k$系统的输出应为：

$$
c(k)=\sum_{i=0}^{k}a(i)b(k-i)
$$

上述公式似乎非常眼熟。设有两个多项式$A(x)$和$B(x)$：

$$
A(x)=a_0+a_1x+a_2x^2+\cdots+a_dx^d
$$

$$
B(x)=b_0+b_1x+b_2x^2+\cdots+b_dx^d
$$

则它们相乘的结果$C(x)=A(x)\cdot B(x)=c_0+c_1x+c_2x^2+\cdots+c_{2d}x^{2d}$的系数满足：

$$
c_k=\sum_{i=0}^{k}a_ib_{k-i}
$$

其中若$i>d$，则令$a_i,b_i=0$。这与系统响应函数的表达式完全相同，我们通常称这个操作为卷积（convolution），记为$c(t)=a(t)*b(t)$。卷积在数字信号处理中非常重要，加快卷积的计算速度也是必然要求。

如果按照上述方法求解两个$d$次多项式的乘法，复杂度为$\Theta(d^2)$，有没有可能降低复杂度呢？如果还是用列举系数来表示一个多项式的话，似乎很难再优化了，我们可以换一种思路，使用点值表示法。

2. 多项式乘法

假设多项式$A(x)$的次数为$n-1$，系数表示法如下：

$$
A(x)=a_0+a_1x+a_2x^2+\cdots+a_{n-1}x^{n-1}
$$

该多项式可以唯一地被$n$个不同的点所确定，即：

$$
{(x_0,y_0),(x_1,y_1),\cdots,(x_{n-1},y_{n-1})}
$$

其中，$y_k=A(x_k),(k=0,1,\cdots,n-1)$且$x_k$各不相同。

$Proof$：本质上就是解如下的矩阵方程：

$$
\begin{equation}
\begin{bmatrix}
1 & x_0 & x_0^2 & \cdots & x_0^{n-1} \\ 1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{n-1}^{n-1} \
\end{bmatrix}
\begin{bmatrix}
a_0 \\ a_1 \\ \vdots \\ a_{n-1} \
\end{bmatrix}
=
\begin{bmatrix}
y_0 \\ y_1 \\ \vdots \\ y_{n-1} \
\end{bmatrix}
\end{equation}
$$

左边的矩阵为范德蒙矩阵，因为$x_k$各不相同，该矩阵一定可逆，故可以确定唯一的一组系数向量$\mathbb{a}$。▮

如果我们一直使用点值表示法来描述多项式，那么多项式的乘法就变得非常简单了，直接对两组点做点值乘法。但是这样只能得到$n$个点，而得到的多项式应该是$2n-2$次的，故需要先对点值做扩展：

$$
A(x):{(x_0,y_0),(x_1,y_1),\cdots,(x_{2n-1},y_{2n-1})}
$$

$$
B(x):{(x_0,y_0’),(x_1,y_1’),\cdots,(x_{2n-1},y_{2n-1}’)}
$$

$$
C(x)=A(x)\cdot B(x):{(x_0,y_0y_0’),(x_1,y_1y_1’),\cdots,(x_{2n-1},y_{2n-1}y_{2n-1}’)}
$$

使用这个方法，多项式乘法的复杂度就能降到$\Theta(n)$。不幸的是，我们很少使用点值表示法，因为我们通常需要计算多项式在任意点处的值，而点值表示法只能给出$n$个点的值。

换个思路，我们可以只在实行多项式乘法的时候使用点值表示法；也就是说，做乘法之前先分别对两个多项式进行$2n$个点的求值（evaluation），将它转化为点值表示，然后做点乘，最后对生成的$2n$个点进行插值(interpolation)，转化为系数表示：

1. 选择：挑选合适的$2n$个点$x_0,x_1,\cdots,x_{2n-1}$。
2. 求值：计算$A(x_0),A(x_1),\cdots,A(x_{2n-1})$和$B(x_0),B(x_1),\cdots,B(x_{2n-1})$。
3. 点乘：$C(x_k)=A(x_k)\cdot B(x_k)$。
4. 插值：恢复$C(x)=c_0+c_1x+\cdots+c_{2n-2}x^{2n-2}$。

使用这个方法，我们的主要矛盾就转移到了如何降低求值和插值的复杂度，整个算法的复杂度也取决于这两个步骤。

3. 多项式求值

对于多项式$A(x)$，给定$n$个不同的点$x_0,x_1,\cdots,x_{n-1}$，如何快速的求出$A(x_0),A(x_1),\cdots,A(x_{n-1})$是我们现在要解决的问题。使用霍纳法则：

$$
A(x_k)=a_0+x_k(a_1+x_k(a_2+\cdots+x_k(a_{n-2}+x_ka_{n-1})\cdots))
$$

求每个点的值花费$\Theta(n)$，求出全部的点的值需要$\Theta(n^2)$，仍然是太慢了。但是我们忽略了一点，我们是可以随意选择这些求值点的，是否存在某种选择方法可以让求值更快一些？

假设$n$为2的幂（若不是，就将多项式系数补零到刚大于$n$的那个2的幂），我们挑选这样的$n$个点：

$$
x_0,x_1,\cdots,x_{n/2-1}
$$

$$
-x_0,-x_1,\cdots,-x_{n/2-1}
$$

我们把$A(x)$按照系数位置下标的奇偶性分成两个部分：

$$
A_e(x^2)=a_0+a_2x^2+\cdots+a_{n-2}x^{n-2}
$$

$$
xA_o(x^2)=a_1x+a_3x^3+\cdots+a_{n-1}x^{n-1}
$$

则$A(x)$可以被表示为：

$$
A(x)=A_e(x^2)+xA_o(x^2)
$$

可以观察到：

$$
A(x_i)=A_e(x_i^2)+x_iA_o(x_i^2)
$$

$$
A(-x_i)=A_e(x_i^2)-x_iA_o(x_i^2)
$$

这说明，为了计算$A(x)$在$\pm x_0,\pm x_1,\cdots,\pm x_{n/2-1}$（$n$个点）处的值，我们只需要分别计算$A_e(x^2)$和$A_o(x^2)$在$x_0^2,x_1^2,\cdots,x_{n/2-1}^2$（$n/2$个点）处的值，即把一个大小为$n$的问题转化为了两个大小为$n/2$的子问题。如果该分治策略能够顺利进行下去，将有如下的递归关系式：

$$
T(n)=2T(n/2)+\Theta(n)
$$

最终的复杂度将为$\Theta(n\log n)$，确实大大降低。

但是这个方法只能分治一次，第一次分治我们利用加减号的对称性，将问题规模降到一半。第二次分治，我们需要对$x_0^2,x_1^2,\cdots,x_{n/2-1}^2$求值，但是我们再也不能找到一种分割方法，仅对一半点求值，就能计算出全部点的值。原因很显然，平方操作让这种加减对称性消失了。是否存在某些点，对其进行平方，仍然存在某种对称性？那就必须要引入复数了。

设复数$\omega$满足方程$\omega^n=1$，$n$次单位复数根恰好有$n$个，这些根为：

$$
\omega_n^k=e^{2\pi ik/n}
$$

我们称$\omega_n=e^{2\pi i/n}$为主$n$次单位根，其余根都是它的幂次。

若我们选取$\omega_n^0,\omega_n^1,\omega_n^2,\cdots,\omega_n^{n-1}$作为$n$个求值点，则可以推出：

$$
\begin{equation}
\begin{aligned}
A(\omega_n^k)
& = A_e(\omega_n^{2k})+\omega_n^kA_o(\omega_n^{2k}) \\ &= A_e(\omega_{n/2}^{k})+\omega_n^kA_o(\omega_{n/2}^{k})
\end{aligned}
\end{equation}
$$

$$
\begin{equation}
\begin{aligned}
A(\omega_n^{k+n/2})
& = A_e(\omega_n^{2k+n})+\omega_n^{k+n/2}A_o(\omega_n^{2k+n}) \\ &= A_e(\omega_{n}^{2k})-\omega_n^kA_o(\omega_{n}^{2k}) \\ &= A_e(\omega_{n/2}^{k})-\omega_n^kA_o(\omega_{n/2}^{k})
\end{aligned}
\end{equation}
$$

其中$k=0,1,2,\cdots,n/2-1$。

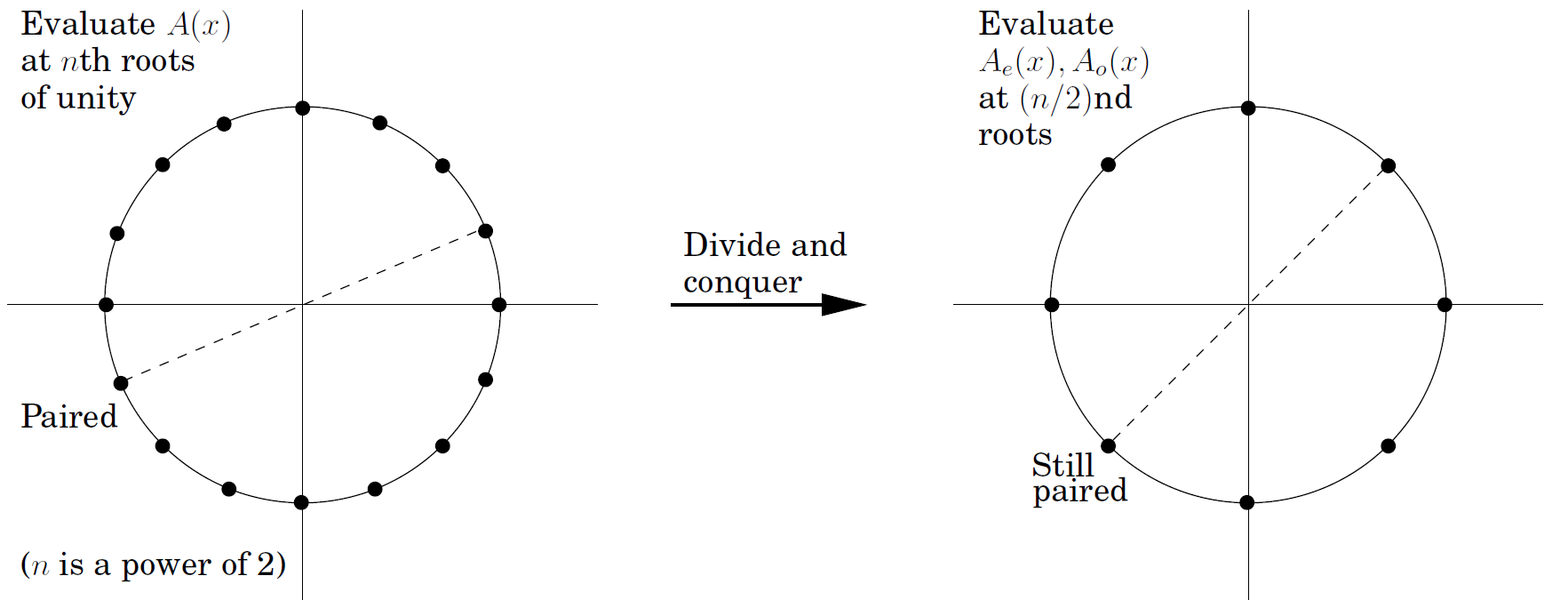
为了计算$A(x)$在$\omega_n^0,\omega_n^1,\omega_n^2,\cdots,\omega_n^{n-1}$（$n$个点）处的值，我们只需要分别计算$A_e(x^2)$和$A_o(x^2)$在$\omega_{n/2}^0,\omega_{n/2}^1,\omega_{n/2}^2,\cdots,\omega_{n/2}^{n/2-1}$（$n/2$个点）处的值，并且可以一直分治下去。该算法的复杂度为$O(n\log n)$。

4. 快速傅里叶变换（FFT）

假设有$n-1$次多项式$A(x)$：

$$
A(x)=\sum_{j=0}^{n-1}a_jx^j
$$

计算$A(x)$在$n$个$n$次单位复数根$\omega_n^0,\omega_n^1,\omega_n^2,\cdots,\omega_n^{n-1}$处的值，定义结果$y_k$：

$$
y_k=A(x_n^k)=\sum_{j=0}^{n-1}a_j\omega_n^{kj}
$$

则我们称向量$\mathbb{y}=(y_0,y_1,\cdots,y_{n-1})$就是系数向量$\mathbb{a}=(a_0,a_1,\cdots,a_{n-1})$的离散傅里叶变换（Discrete Fourier Transform, DFT），记为$y=DFT_n(\mathbb{a})$。（其他数字信号处理教材中，$\omega_n^{ki}$应该为$\omega_n^{-ki}$，算法导论里的没有负号，不过不影响）

我们按上述方法对多项式进行求值，其实就是对多项式系数做了一次DFT；采用上述分治法和利用复数根特殊性质来求解DFT的过程，被称为快速傅里叶变换（Fast Fourier Transform, FFT）。递归公式：

$$
\begin{equation}
\begin{aligned}
y[k]
& = y_e[k]+\omega_n^ky_o[k]
\end{aligned}
\end{equation}
$$

$$
\begin{equation}
\begin{aligned}
y[n/2+k]
& = y_e[k]-\omega_n^ky_o[k]
\end{aligned}
\end{equation}
$$

下面是使用递归法求解向量$\mathbb{a}=(a_0,a_1,\cdots,a_{n-1})$的FFT的步骤：

do_recursive_FFT(a):
	n = a.length
	if n==1: return a
	w_n为主n次单位根
	w = 1
	
	a_e = [a[0], a[2], ..., a[n-2]]
	a_o = [a[1], a[3], ..., a[n-1]]
	y_e = do_recursive_FFT(a_e)
	y_o = do_recursive_FFT(a_o)
	
	for k=0 to n/2-1:
		y[k] = y_e[k] + w*y_o[k]
		y[k+n/2] = y_e[k] - w*y_o[k]
		w = w * w_n
	return y

下面我们再从矩阵的角度整体回顾一下FFT的原理。

对多项式$A(x)$在$x_0,x_1,\cdots,x_{n-1}$处取值，可以写成矩阵形式：

$$
\begin{equation}
\begin{bmatrix}
y_0 \\ y_1 \\ \vdots \\ y_{n-1}
\end{bmatrix}
=
\begin{bmatrix}
1 & x_0 & x_0^2 & \cdots & x_0^{n-1} \\ 1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{n-1}^{n-1}
\end{bmatrix}
\begin{bmatrix}
a_0 \\ a_1 \\ \vdots \\ a_{n-1}
\end{bmatrix}
\end{equation}
$$

记矩阵为$M$。若在$n$个$n$次单位复数根$\omega_n^0,\omega_n^1,\omega_n^2,\cdots,\omega_n^{n-1}$处取值，即做DFT操作，则可以表达为：

$$
\begin{equation}
\begin{bmatrix}
y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1}
\end{bmatrix}
=
\begin{bmatrix}
1 & 1 & 1 & 1 & \cdots & 1\\ 1 & \omega_n^{1} & \omega_n^{2} & \omega_n^{3} & \cdots & \omega_n^{n-1} \\ 1 & \omega_n^{2} & \omega_n^{4} & \omega_n^{6} & \cdots & \omega_n^{2(n-1)} \\ 1 & \omega_n^{3} & \omega_n^{6} & \omega_n^{9} & \cdots & \omega_n^{3(n-1)} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \omega_n^{3(n-1)} & \cdots & \omega_n^{(n-1)(n-1)}
\end{bmatrix}
\begin{bmatrix}
a_0 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_{n-1}
\end{bmatrix}
\end{equation}
$$

记矩阵为$M=M_n(\omega)$，其中$M(j,k)=\omega_n^{jk}$。在FFT算法中，我们首先根据系数下标的奇偶性，把系数分成了两个部分，重新排列系数矩阵的列以及系数向量的行：

$$
\begin{equation}
\begin{bmatrix}
y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1}
\end{bmatrix}
=
\begin{bmatrix}
1 & 1 & 1 & \cdots & 1 & 1 & 1 & \cdots \\ 1 & \omega_n^{2} & \omega_n^{4} & \cdots & \omega_n^{1} & \omega_n^{3} & \omega_n^{5} & \cdots \\ 1 & \omega_n^{4} & \omega_n^{8} & \cdots & \omega_n^{2} & \omega_n^{6} & \omega_n^{10} & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & \omega_n^{2n/2} & \omega_n^{4n/2} & \cdots & \omega_n^{n/2} & \omega_n^{3n/2} & \omega_n^{5n/2} & \cdots \\ 1 & \omega_n^{2n/2+2} & \omega_n^{4n/2+4} & \cdots & \omega_n^{n/2+1} & \omega_n^{3n/2+3} & \omega_n^{5n/2+5} & \cdots \\ 1 & \omega_n^{2n/2+4} & \omega_n^{4n/2+8} & \cdots & \omega_n^{n/2+2} & \omega_n^{3n/2+6} & \omega_n^{5n/2+10} & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots
\end{bmatrix}
\begin{bmatrix}
a_0 \\ a_2 \\ a_4 \\ \vdots \\ a_1 \\ a_3 \\ a_5 \\ \vdots
\end{bmatrix}
\end{equation}
$$

利用复数根的性质，继续化简上式：

$$
\begin{equation}
\begin{bmatrix}
y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1}
\end{bmatrix}
=
\begin{bmatrix}
1 & 1 & 1 & \cdots & \omega_n^{0}\cdot 1 & \omega_n^{0}\cdot1 & \omega_n^{0}\cdot1 & \cdots \\ 1 & \omega_n^{2} & \omega_n^{4} & \cdots & \omega_n^{1}\cdot 1 & \omega_n^{1}\cdot\omega_n^{2} & \omega_n^{1}\cdot\omega_n^{4} & \cdots \\ 1 & \omega_n^{4} & \omega_n^{8} & \cdots & \omega_n^{2}\cdot 1 & \omega_n^{2}\cdot\omega_n^{4} & \omega_n^{2}\cdot\omega_n^{8} & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & 1 & 1 & \cdots & \omega_n^{n/2}\cdot 1 & \omega_n^{n/2}\cdot 1 & \omega_n^{n/2}\cdot 1 & \cdots \\ 1 & \omega_n^{2} & \omega_n^{4} & \cdots & \omega_n^{n/2+1}\cdot 1 & \omega_n^{n/2+1}\cdot\omega_n^{2} & \omega_n^{n/2+1}\cdot\omega_n^{4} & \cdots \\ 1 & \omega_n^{4} & \omega_n^{8} & \cdots & \omega_n^{n/2+2}\cdot 1 & \omega_n^{n/2+2}\cdot\omega_n^{4} & \omega_n^{n/2+2}\cdot\omega_n^{8} & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots
\end{bmatrix}
\begin{bmatrix}
a_0 \\ a_2 \\ a_4 \\ \vdots \\ a_1 \\ a_3 \\ a_5 \\ \vdots
\end{bmatrix}
\end{equation}
$$

观察发现，上式中的矩阵可以分成四个部分，每个部分都含有一个公共的矩阵$M_{n/2}(\omega^2)$：

$$
\begin{equation}
\begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1} \end{bmatrix} = \begin{bmatrix} \begin{bmatrix} 1 & 1 & 1 & \cdots \\ 1 & \omega_n^{2} & \omega_n^{4} & \cdots \\ 1 & \omega_n^{4} & \omega_n^{8} & \cdots \\ \vdots & \vdots & \vdots & \ddots \end{bmatrix} \begin{bmatrix} a_0 \\ a_2 \\ a_4 \\ \vdots \end{bmatrix} + \begin{bmatrix} \omega_n^{0} \\ \omega_n^{1} \\ \omega_n^{2} \\ \vdots \end{bmatrix}^T \begin{bmatrix} 1 & 1 & 1 & \cdots \\ 1 & \omega_n^{2} & \omega_n^{4} & \cdots \\ 1 & \omega_n^{4} & \omega_n^{8} & \cdots \\ \vdots & \vdots & \vdots & \ddots \end{bmatrix} \begin{bmatrix} a_1 \\ a_3 \\ a_5 \\ \vdots
\end{bmatrix} \\ \begin{bmatrix} 1 & 1 & 1 & \cdots \\ 1 & \omega_n^{2} & \omega_n^{4} & \cdots \\ 1 & \omega_n^{4} & \omega_n^{8} & \cdots \\ \vdots & \vdots & \vdots & \ddots \end{bmatrix} \begin{bmatrix} a_0 \\ a_2 \\ a_4 \\ \vdots \end{bmatrix} - \begin{bmatrix}
\omega_n^{0} \\ \omega_n^{1} \\ \omega_n^{2} \\ \vdots \end{bmatrix}^T \begin{bmatrix} 1 & 1 & 1 & \cdots \\ 1 & \omega_n^{2} & \omega_n^{4} & \cdots \\ 1 & \omega_n^{4} & \omega_n^{8} & \cdots \\ \vdots & \vdots & \vdots & \ddots \end{bmatrix} \begin{bmatrix} a_1 \\ a_3 \\ a_5 \\ \vdots \end{bmatrix} \end{bmatrix} \end{equation}
$$

即：

$$
\begin{equation} \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1} \end{bmatrix} = M_n(\omega) \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ a_4 \\ \vdots \\ a_{n-1} \end{bmatrix} = \begin{bmatrix} M_{n/2}(\omega^2) \begin{bmatrix} a_0 \\ a_2 \\ a_4 \\ \vdots \end{bmatrix} + \begin{bmatrix} \omega_n^{0} \\ \omega_n^{1} \\ \omega_n^{2} \\ \vdots \end{bmatrix}^T M_{n/2}(\omega^2) \begin{bmatrix} a_1 \\ a_3 \\ a_5 \\ \vdots \end{bmatrix} \\ M_{n/2}(\omega^2) \begin{bmatrix} a_0 \\ a_2 \\ a_4 \\ \vdots \end{bmatrix} - \begin{bmatrix} \omega_n^{0} \\ \omega_n^{1} \\ \omega_n^{2} \\ \vdots \end{bmatrix}^T M_{n/2}(\omega^2) \begin{bmatrix} a_1 \\ a_3 \\ a_5 \\ \vdots \end{bmatrix} \end{bmatrix} \end{equation}
$$

观察发现，FFT的本质就是把$M_n(\omega)$乘以向量$(a_0,a_1,\cdots,a_{n-1})^T$的问题转化成了$M_{n/2}(\omega^2)$乘以向量$(a_0,a_2,\cdots,a_{n-2})^T$和$M_{n/2}(\omega^2)$乘以向量$(a_1,a_3,\cdots,a_{n-1})^T$的两个子问题，有如下的递归关系式：

$$
T(n)=2T(n/2)+\Theta(n)
$$

最终的复杂度为$\Theta(n\log n)$。

5. 高效FFT实现

在实际应用中，DFT同时要求较低的时间和空间复杂度，FFT的递归实现占用大量空间，下面介绍FFT的迭代实现方法，将比递归版快一些，而且占用更少的空间。

首先分析一下递归FFT的运行过程，画出如下的递归树：

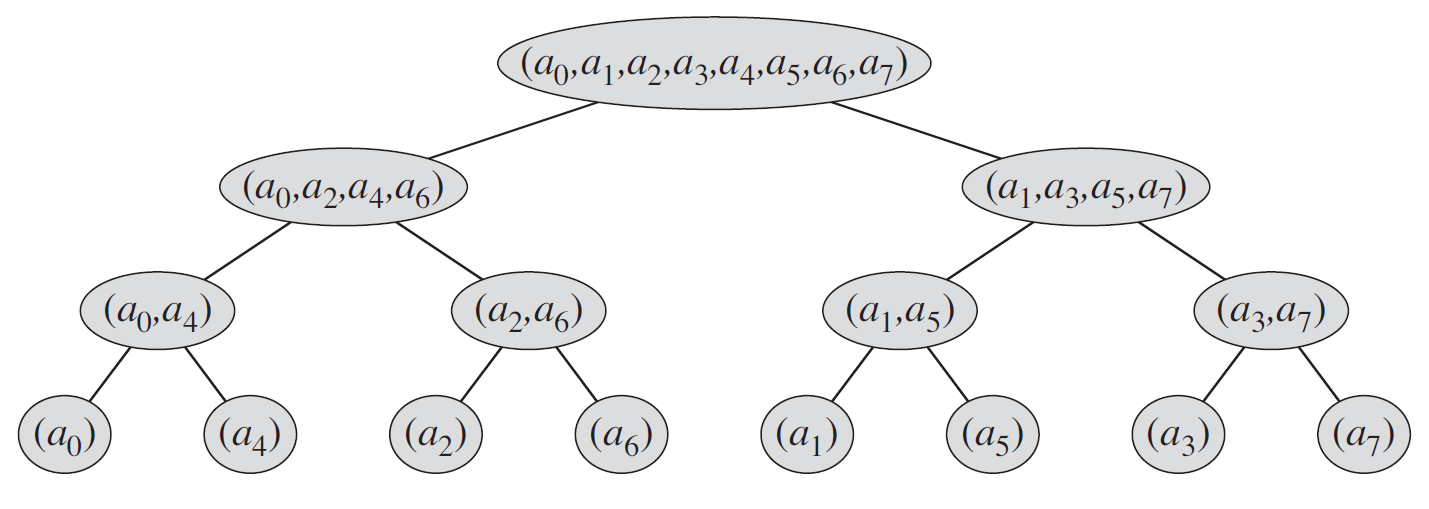
我们需要模拟递归中自底向上的计算过程。首先注意到，数组元素的次序在最底层是被打乱的，出现的顺序是原数组的位逆序置换。比如做8点DFT时，最底层的第001（1）个元素应该是原数组的第100（4）个元素。实际操作中，通常提前准备好bit-reverse lookup table，达到$O(1)$的位逆序置换速度。

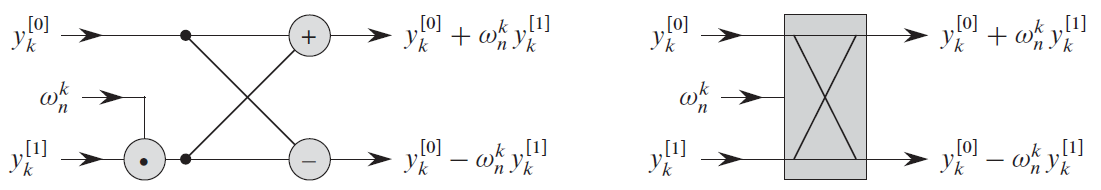
从最底层开始，成对取出元素，做一次蝴蝶操作计算出每对的DFT，用其DFT取代这对元素：

$$
t =\omega_n^ky_o[k]
$$

$$
\begin{equation}
\begin{aligned}
y[k]
& = y_e[k]+t
\end{aligned}
\end{equation}
$$

$$
\begin{equation}
\begin{aligned}
y[n/2+k]
& = y_e[k]-t
\end{aligned}
\end{equation}
$$

这样向量中就包含了$n/2$个二元素的DFT。然后，按对取出这$n/2$个元素的DFT，通过两次蝴蝶操作计算出四元素向量的DFT。以此类推，最终我们就得到了一个具有$n$元素的DFT。

设当前自底向上所处递归树的层次为$s$，最底层为$s=1$，则每次应该取出$m=2^s$个元素做蝴蝶操作。每次蝴蝶操作就是把$A[k:k+m/2-1]$和$A[k+m/2:k+m-1]$两个数组合并成$A[k:k+m-1]$。伪代码如下：

do_iterative_FFT(a):
	A = bit_reverse(a)
	n = a.length
	for s=1 to log2(n):
		m = 2^s
		w_m为主m次单位根
		for k = 0 to n-1 by m:
			w = 1
			for j = 0 to m/2-1:
				u = A[k+j]
				t = A[k+m/2+j]
				A[k+j] = u + t
				A[k+m/2+j] = u - t
				w = w * w_m
return A

复杂度计算：

$$
T(n)=\sum_{s=1}^{\log n}\frac{n}{2^s}\cdot 2^{s-1}=\Theta(n\log n)
$$

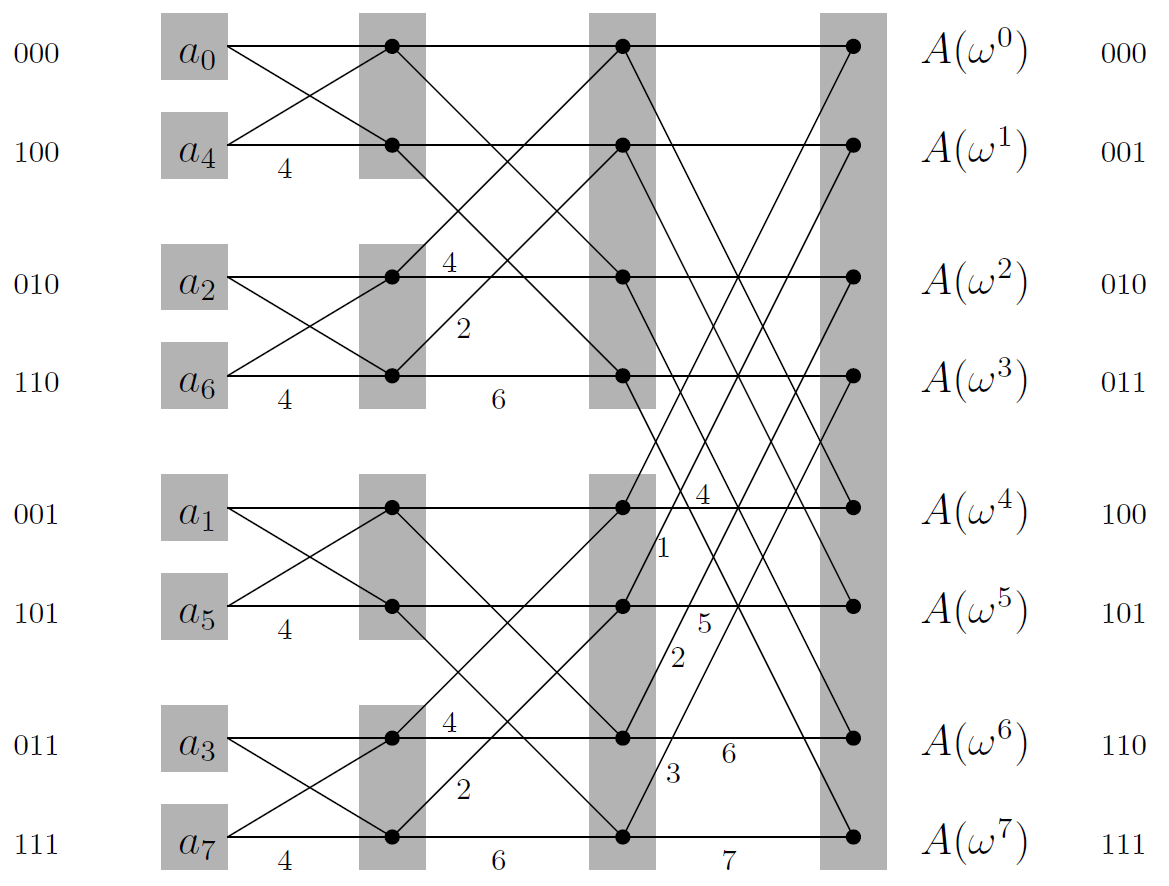
再次观察递归树，我们发现每一层的计算其实可以改为并行操作，因为它们之间没有依赖性。故可以设计出下面的并行FFT电路，深度为$\Theta(\log n)$级，这也是实际硬件中使用的电路模型：

5. 多项式插值与IFFT

回到多项式乘法的主题上来，我们使用了FFT使对$2n$个点求值这一步的复杂度降低到了$\Theta(n\log n)$，之后对这$2n$个点进行点乘。现在还差最后一步操作，就是对$2n$个点插值，得到乘积多项式的系数向量。再次回顾一下这个等式：

$$
\begin{equation}
\begin{bmatrix}
y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1}
\end{bmatrix}
=
\begin{bmatrix}
1 & 1 & 1 & 1 & \cdots & 1\\ 1 & \omega_n^{1} & \omega_n^{2} & \omega_n^{3} & \cdots & \omega_n^{n-1} \\ 1 & \omega_n^{2} & \omega_n^{4} & \omega_n^{6} & \cdots & \omega_n^{2(n-1)} \\ 1 & \omega_n^{3} & \omega_n^{6} & \omega_n^{9} & \cdots & \omega_n^{3(n-1)} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \omega_n^{3(n-1)} & \cdots & \omega_n^{(n-1)(n-1)}
\end{bmatrix}
\begin{bmatrix}
a_0 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_{n-1}
\end{bmatrix}
\end{equation}
$$

现在我们知道了$\mathbb{y}$和$M_n(\omega)$，需要求出$\mathbb{a}$。由于$M_n(\omega)$一定可逆，所以：

$$
\begin{equation}
\begin{bmatrix}
a_0 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_{n-1}
\end{bmatrix}
=
M_n(\omega)^{-1}
\begin{bmatrix}
y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1}
\end{bmatrix}
\end{equation}
$$

那么$M_n(\omega)$的逆矩阵等于多少呢？我们构造一个矩阵$M_n(\omega)^*$，里面的每个元素都是$M_n(\omega)$对应元素的共轭。那么$M_n(\omega)M_n(\omega)^*$的$(j,k)$位置元素的值为：

$$
1+\omega_n^{j-k}+\omega_n^{2(j-k)}+\omega_n^{3(j-k)}+\cdots+\omega_n^{(n-1)(j-k)}
$$

当$j=k$时，结果为$n$；当$j\neq k$时，结果为$(1-\omega_n^{n(j-k)})/(1-\omega_n^{j-k})=0$，这说明$M_n(\omega)$的所有列都是互相正交的。我们发现：

$$
M_n(\omega)M_n(\omega)^*=nI
$$

可以看出，$M_n(\omega)^{-1}=\frac{1}{n}M_n(\omega)^*=\frac{1}{n}M_n(\omega^{-1})$。利用这个结论，可以直接写出逆DFT的表达式：

$$
\mathbb{a}=DFT^{-1}_n(\mathbb{y})
$$

$$
a_k=\frac{1}{n}\sum_{j=0}^{n-1}y_j\omega_n^{-jk}
$$

计算逆FFT的方式很简单，在原FFT程序中将$\mathbb{a}$和$\mathbb{y}$互换，用$\omega_n^{-1}$替换$\omega_n$，并将计算结果的每个元素都除以$n$即可。复杂度仍然是$\Theta(n\log n)$。

总结一下，多项式乘法的过程可以用卷积定理来说明：

对于任意两个向量$\mathbb{a}$和$\mathbb{b}$，将它们的长度补零至$2n$，$n$为2的幂，则：

$$
\mathbb{a}*\mathbb{b}=DFT_{2n}^{-1}(DFT_{2n}(\mathbb{a})\cdot DFT_{2n}(\mathbb{b}))
$$

其中$*$表示卷积，$\cdot$表示点乘。计算DFT的过程可以使用FFT算法。

下面的图也清晰地描述了使用FFT求解多项式乘法的过程：

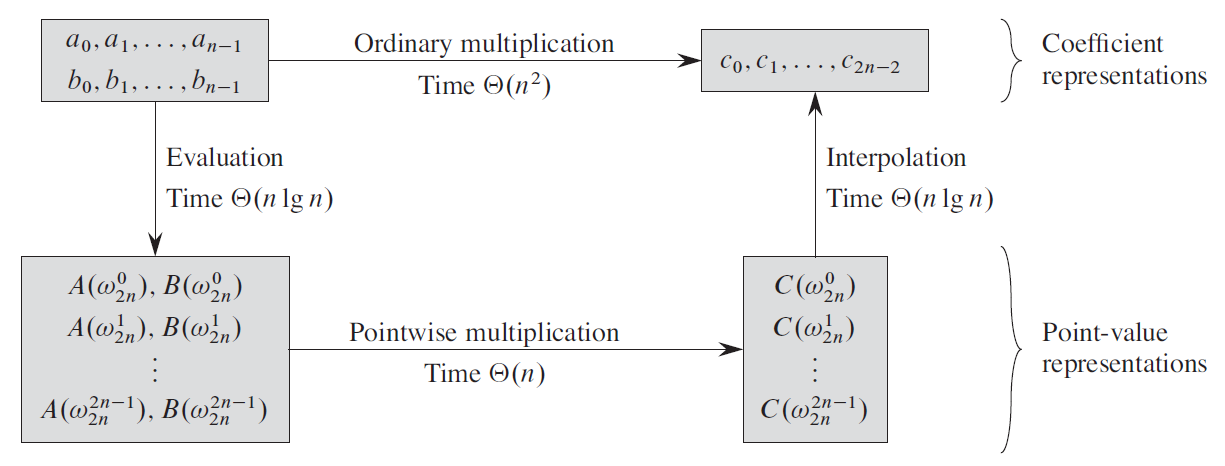
我们把多项式中的$x$换成$2$或者$10$，可以发现多项式的系数向量可以表示一个以2或10为base的数，这就意味着可以使用FFT求解整数乘法，复杂度为$\Theta(n\log n)$，比以前介绍过的任何一种乘法算法都要快！

Quick Link: 算法笔记整理