chap 2-2 分治算法-排序和选择

    Blog  0 visits

1. 快速排序（Quicksort）

排序算法经常用到分治策略。在现实中，最常用的排序算法当属快速排序。主要过程：首先进行partition操作，从数组中挑选一个元素作为主元pivot，将小于pivot的元素放置到它的左边，将大于pivot的元素放置到它的右边；然后递归地对pivot左右两边的数组进行partition。

具体实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int partition(int* a, int l, int r) {
	int p = a[r - 1];
	int i = l - 1;
	for (int j = l; j < r - 1; ++j) {
		if (a[j] <= p) {
			i++;
			swap(a, i, j);
		}
	}
	swap(a, i + 1, r - 1);
	return i + 1;
}

void quicksort(int* a, int l, int r) {
	if (r - l >= 2) {
		int m = partition(a, l, r);
		quicksort(a, l, m);
		quicksort(a, m + 1, r);
	}
}

下面进行复杂度的分析，由于复杂度与选择的pivot有关，所以我们要逐一分析最坏、最好和平均的复杂度。

最坏情况复杂度：每次partition时都出现了极其不平衡的划分，分出了大小为$0$和$n-1$的两个子问题，递归表达式如下：

$$
T(n)=T(0)+T(n-1)+\Theta(n)=T(n-1)+\Theta(n)
$$

故最坏情况的复杂度为$\Theta(n^2)$。

最好情况复杂度：每次partition时都出现了恰好平衡的划分，递归表达式如下：

$$
T(n)=2T(n/2)+\Theta(n)
$$

故最好情况的复杂度为$\Theta(n\log n)$。

平均情况复杂度：假设输入的数据完全是随机的，则每个元素成为主元的概率为$1/n$（$n$为本次划分的数组的大小）。若挑选的主元在数组中排第$i$位，则子问题的大小为$i-1$和$n-i$，列出以下递归表达式：

$$
T(n)=\frac{1}{n}\sum_{i=1}^{n}[T(i-1)+T(n-i)+O(n)]=O(n)+\frac{2}{n}\sum_{i=1}^{n-1}T(i)
$$

则：

$$
T(n-1)=O(n-1)+\frac{2}{n-1}\sum_{i=1}^{n-2}T(i)
$$

联合两个式子，可得：

$$
\begin{equation}
\begin{aligned}
T(n) & = \frac{n+1}{n}T(n-1)+O(1) \\ & =O(1)(1+\frac{n+1}{n}+\frac{n+1}{n-1}+\frac{n+1}{n-2}+\cdots+\frac{n+1}{1}) \\ &=O(1)[1+(n+1)\sum_{i=1}^n\frac{1}{i}] \\ &= O(n\log n)
\end{aligned}
\end{equation}
$$

故平均复杂度为$O(n\log n)$。但是这是在我们假定输入数据完全随机的条件下推导出的，在现实中很少会出现这种情况。为了保证较好的平均复杂度，我们每次partition时可以随机选取主元，人工引入随机因素。下面是随机版快速排序的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
int randomized_partition(int* a, int l, int r) {
	int m = rand() % (r - l) + l;
	swap(a, m, r - 1);
	return partition(a, l, r);
}

void randomized_quicksort(int* a, int l, int r) {
	if (r - l >= 2) {
		int m = randomized_partition(a, l, r);
		randomized_quicksort(a, l, m);
		randomized_quicksort(a, m + 1, r);
	}
}

随机版快速排序的良好性能使之成为排序大量数据的首选算法，包括Unix系统内置的文件排序命令。

2. 归并排序（Mergesort）

另一种比较容易想到的方法就是归并排序，主要过程：把数组分成两部分，分别排序好每个部分（子问题），然后进行合并操作（merge），返回排序好的整个数组。

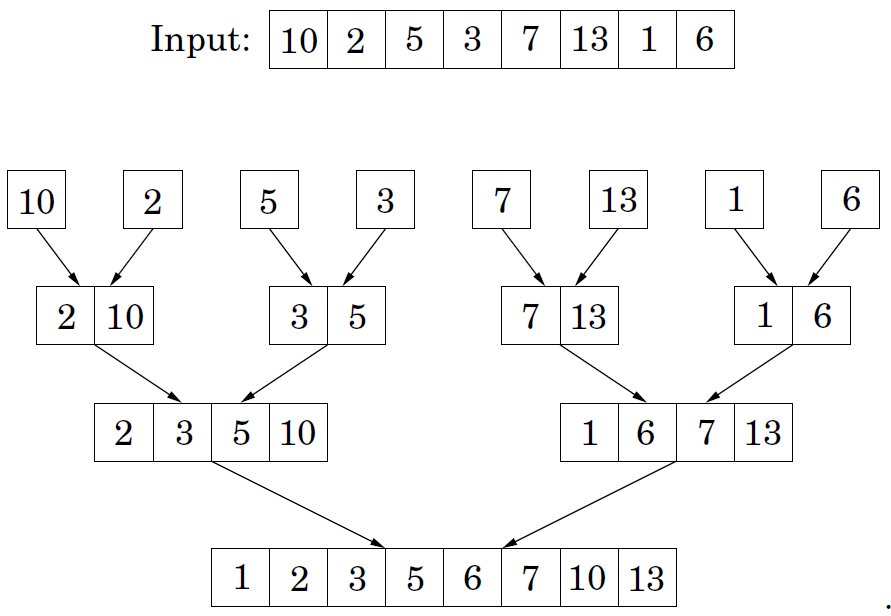
mergesort

伪代码：

1
2
3
4
5
6
7
8
9
10
11
function mergesort(a[1:n]){
	if n>1: return merge(mergesort(a[1:n/2]), mergesort(a[n/2+1, n]))
	else return a
}

function merge(x[1:k], y[1:l]){
	if k=0: return y[1:l]
	if l=0: return x[1:k]
	if x[1]<=y[1]: return x[1] concat merge(x[2:k], y[1:l])
	else: return y[1] concat merge(x[1:k], y[2:l])
}

mergesort(a[1:n/2])和mergesort(a[n/2+1, n])是划分子问题，merge为合并操作。具体实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void merge(int* a, int l, int m, int r) {
	int* left = new int[m - l];
	int* right = new int[r - m];
	for (int i = l; i < m; ++i) left[i - l] = a[i];
	for (int i = m; i < r; ++i) right[i - m] = a[i];
	int i = 0;
	int j = 0;
	int k = l;
	while (i < m - l && j < r - m) {
		if (left[i] <= right[j]) a[k++] = left[i++];
		else a[k++] = right[j++];
	}
	while (i < m - l) a[k++] = left[i++];
	while (j < m - l) a[k++] = right[j++];
	delete[] left;
	delete[] right;
}

// [l, r)
void mergesort(int* a, int l, int r) {
	if (r - l <= 1) return;
	int m = l + (r - l) / 2;
	mergesort(a, l, m);
	mergesort(a, m, r);
	merge(a, l, m, r);
}

下面分析该算法的复杂度，列出递归表达式：

$$
T(n)=2T(n/2)+O(n)
$$

根据主定理，易得复杂度为$O(n\log n)$。

虽然归并排序时间复杂度较低，但是每次归并（merge）操作都要复制数组，占用太多内存，空间复杂度较高。但如果需要排序的数据比内存还大，归并排序的思想就有用武之地了。

3. 外部归并排序（External Mergesort）

假设现在计算机的内存为8GB，硬盘中有128GB的数据需要排序，我们显然不能采取一般的排序方法：直接把数据全部装载到内存，然后一次性排好序，最后存回硬盘。我们可以利用归并排序的思想进行外部排序（external sorting）：每次装载8GB数据到内存，排好序后（快排或其他）存回硬盘，重复16次，硬盘中就有了16个内部有序的子文件；然后对这16个文件进行合并操作，最终生成一个内部有序的大文件。内存中归并排序的不足是需要复制数组，而从硬盘装载数据到内存这一操作必须要复制数组，所以正好适合使用归并排序的思想。

外部归并排序与内存中归并排序的相同点是，都从最初一个个的有序数组开始，一步步合并成最后的一个有序数组；不同点是，外部归并排序最初的有序数组元素很多，而内存中归并排序最初的有序数组中只有一个元素。

下面详细阐述外部归并排序的步骤：

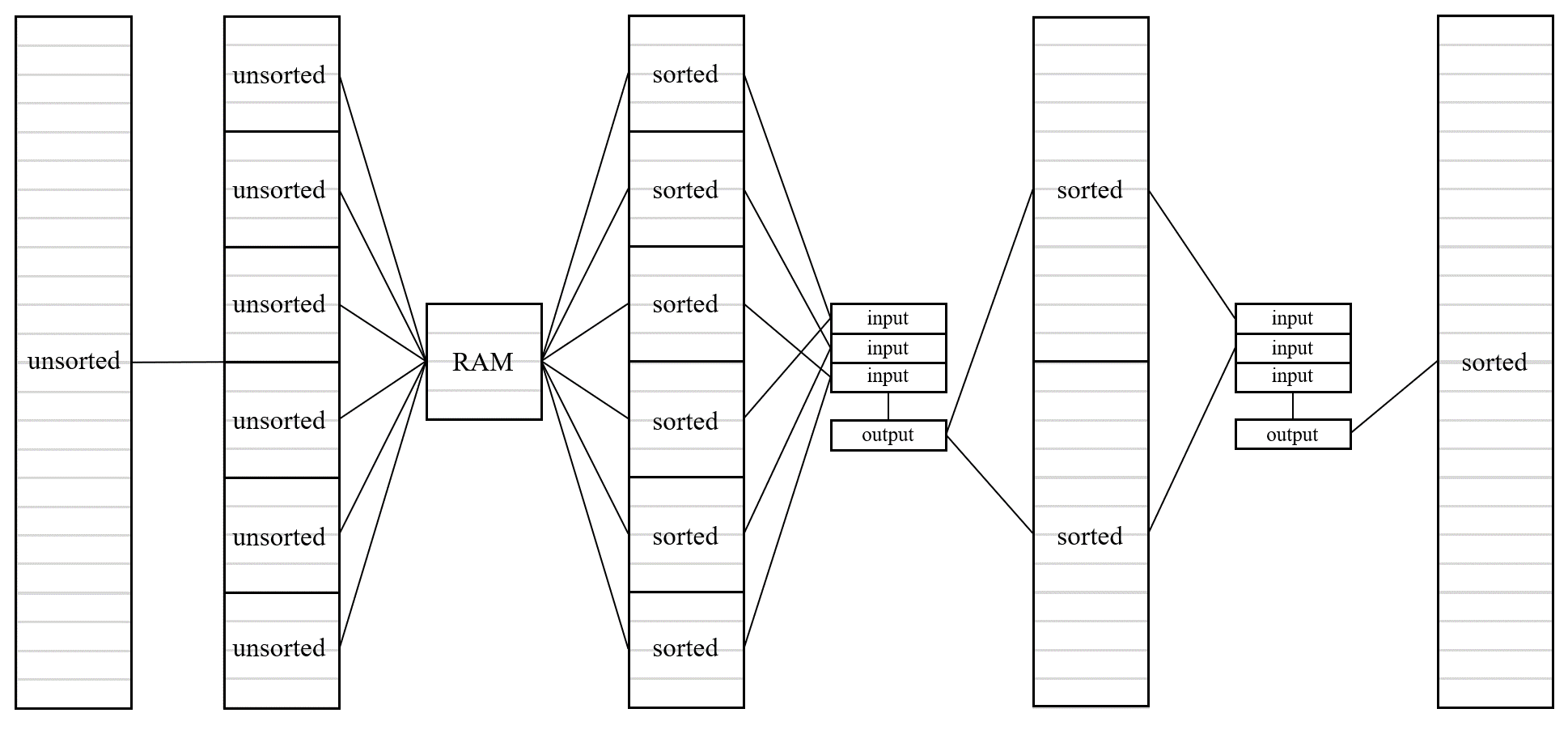
external_mergesort

我们定义一次磁盘I/O传输的数据单元为一个page（假设一个page大小为4KB，在磁盘中通常被称为block），比如从硬盘中取16KB的数据进行排序，然后再写回磁盘，共需8次I/O。给定计算机的内存RAM大小为$B$-page，需要对磁盘中大小为$N$-page的文件进行排序（$N>>B$），可以使用如下的外部归并排序方法。

首先进行conquer：每次从磁盘中装载$B$-pages的数据到RAM中，使用快排或其他方法对该$B$-pages数据进行排序，排序后将其全部写入磁盘中的一个文件中。重复上述步骤直至取完$N$-pages的数据，此时磁盘中应有$\lceil N/B\rceil$个有序的子文件，每个子文件的大小为$B$-page（可能不足$B$-page，下同）。

然后进行merge：现在的目标是将$\lceil N/B\rceil$个大小为$B$-pages的有序子文件合并成1个大小为$N$-pages的大文件。我们将RAM划分成两个部分，一部分是$B-1$个大小为$1$-page的input_buffer，另一部分是1个大小为$1$-page的output_buffer。每个input_buffer关联一个子文件，负责读取子文件中的数据。类比归并排序的合并操作，我们需要从所有input_buffer中找到最小/大的元素填入output_buffer中。若output_buffer填满，则将其中的数据flush到磁盘中的一个文件中；若某一个input_buffer中的数据被读取完，则继续从对应子文件中读入数据，直至所有关联的子文件的数据全被读完。经过上述的一次merge（$B-1$路merge），我们能将$B-1$个有序子文件合并成1个大的有序文件（$B(B-1)$-pages）。经过第一次conquer，生成了$\lceil N/B\rceil$个子文件，如果像上面每次merge了$B-1$个子文件，merge全部$\lceil N/B\rceil$个子文件，则会生成$\lceil \lceil N/B\rceil/(B-1)\rceil$个有序文件。我们称一次完整的上述过程为一个PASS，重复上述过程：

第1个PASS，$\lceil N/B\rceil$个大小为$B$-pages的有序文件合并成了$\lceil \lceil N/B\rceil/(B-1)\rceil$个大小为$B(B-1)$-pages的有序文件；

第2个PASS，$\lceil \lceil N/B\rceil/(B-1)\rceil$个大小为$B$-pages的有序文件合并成了$\lceil \lceil \lceil N/B\rceil/(B-1)\rceil/(B-1)\rceil$个大小为$B(B-1)^2$-pages的有序文件；

……

第$\lceil \log_{B-1}\lceil N/B\rceil\rceil$个PASS，最终只剩了1个大小为$N$-pages的有序文件，完成排序。

下面分析一下该算法耗费的时间，分为CPU计算的时间和磁盘I/O的时间。这里假设每个page含有$p$个元素，内存中排序使用快排，$k$路merge使用最普通的进行$k$次比较选出最小/大元素的方法。

先考虑CPU计算的时间。conquer阶段，进行了$\lceil N/B\rceil$次排序，每次排序的元素个数为$O(Bp)$，则耗费时间为$O(\lceil N/B\rceil Bp\log (Bp))=O(Np\log (Bp))$。每个PASS，output_buffer都一共会输出$Np$个元素，生成每个元素需要$O(B)$，故merge阶段，耗费时间为$O(NBp\lceil \log_{B-1}\lceil N/B\rceil\rceil)=O(NBp\log_B N)$。

再考虑磁盘I/O的时间。conquer和每个PASS，都需要读取和写入$N$-pages，故总的I/O次数为$2N(1+\lceil \log_{B-1}\lceil N/B\rceil\rceil)$。

分析可以发现，$N$和$p$大小不变时，增加$B$可以大大减少磁盘I/O的次数，但是却使merge操作耗费的时间大大增加，最终可能抵消了减少磁盘I/O带来的好处。实际测试中也发现，当$N$很大时，merge操作通常是性能瓶颈。其实有不少关于$k$路merge的优化方案，比如败者树等等，可以大大提升merge的性能，此处不再赘述。

4. 排序算法的下界

研究了这么久排序，那么排序算法最快能有多快呢？其实上述的所有排序，都可以用决策树模型来描述：

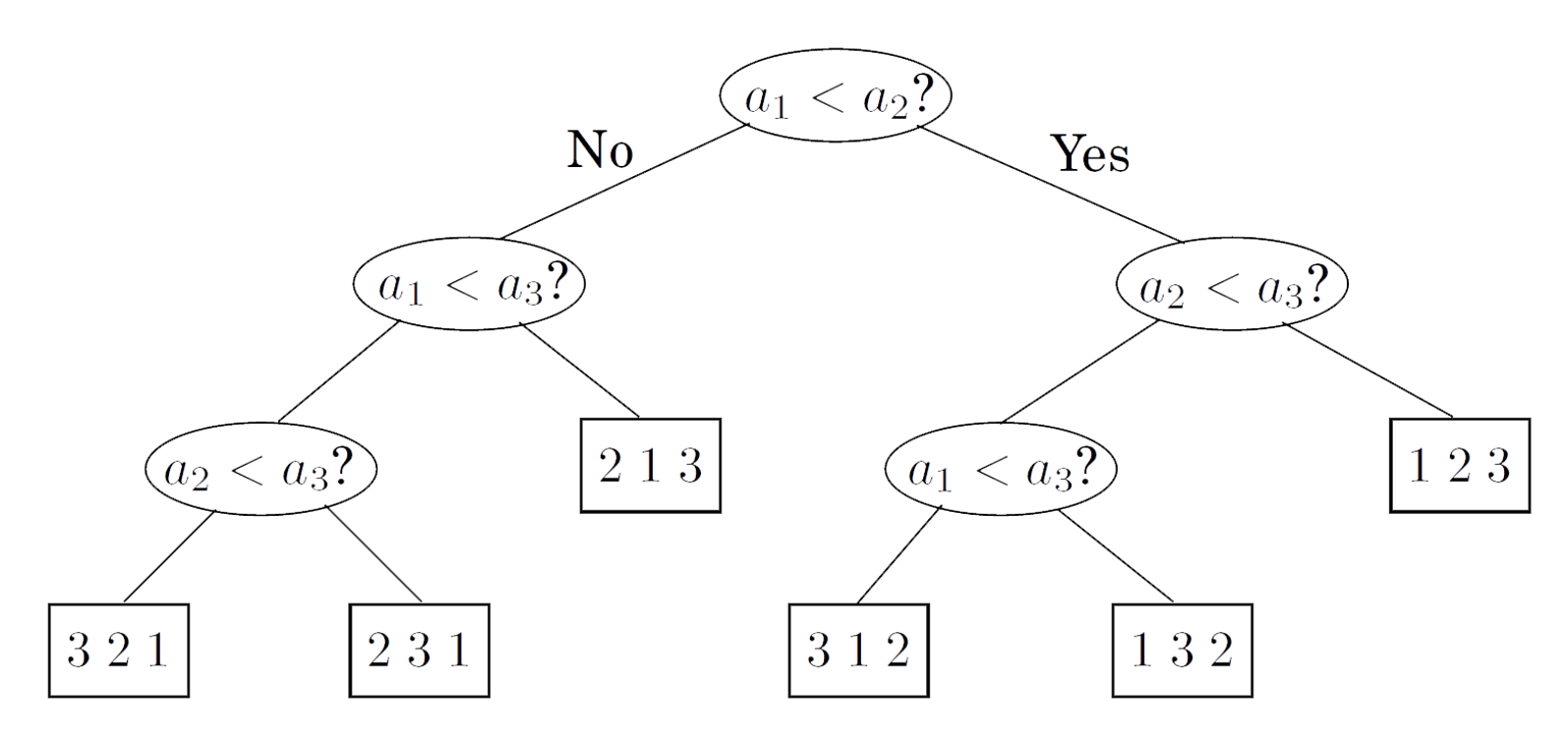
sorting_tree

每一次排序，算法在做的事情都是寻找从根节点到叶节点的一条路径，叶节点就是排序的结果。这棵二叉树的深度就是最坏情况下我们需要比较的次数，可能的最小深度即是排序算法的下界。

通过观察我们发现，若输入数组长度为$n$，那么叶节点的数量至少为$n!$个。反证法，若某个排列不是叶节点，我们总能构造出一个符合这个排列的输入数组，与假设矛盾。因此，若该二叉树的深度为$d$，则它至多有$2^d$个叶节点，又因为叶节点的数量至少为$n!$个，则$n!\leq 2^d$，可以推出$d=\Omega(\log (n!))=\Omega(n\log n)$。

综上所述，基于比较的排序算法的下界为$\Omega(n\log n)$。注意该结论成立的前提是，我们使用比较的方法确定顺序。若数据满足一定的条件，我们甚至可以在线性时间内完成排序，比如计数排序、基数排序等等。

5. 快速选择算法

有些时候，我们并不需要对数据进行排序，我们可能只想知道最大的是哪个，中位数是哪个，最小的是哪个等等。我们需要设计一个选择算法select，返回数组中排名第$k$的元素。回想快速排序，我们选择主元，然后把比它小的和比它大的都排到它左右两边，如果$k$比主元的索引还小，那排名第$k$的元素必然在左边的数组。

受到快排的启发，我们可以设计如下的快速选择算法，同样利用了分治，令$S$为输入的数组，令主元为$v$，$S_L$为比$v$小的子数组，$S_R$为比$v$大的子数组，$S_v$为值都等于$v$的子数组，则排名为第$k$为的元素值为：

$$
\begin{equation}
select(S, k)=
\begin{cases}
select(S_L,k), & k\leq|S_L| \\ v, & |S_L|<k\leq|S_L|+|S_v| \\ select(S_R,k), & k>|S_L|+|S_v|
\end{cases}
\end{equation}
$$

具体实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
pair<int, int> split(int* a, int l, int r, int val) {
	int k = l;
	for (int i = l; i < r; ++i) {
		if (a[i] < val) {
			swap(a, k, i);
			k++;
		}
	}
	int lb = k;
	for (int i = k; i < r; ++i) {
		if (a[i] == val) {
			swap(a, k, i);
			k++;
		}
	}
	int ub = k;
	return make_pair(lb, ub);
}

// k'th smallest element, in place, original array will change
int quickselect(int* a, int l, int r, int k) {
	int val = a[rand() % (r - l) + l];
	pair<int, int> res = split(a, l, r, val);
	int lb = res.first; int ub = res.second;
	if (k <= lb - l) return quickselect(a, l, lb, k);
	else if (k > ub - l) return quickselect(a, ub, r, k - ub + l);
	else return val;
}

我们用split()代替了partition()，二者功能基本相同，但split()可以处理有多个相同主元的情况，返回相同主元区域的左右边界。上述代码实现的split()操作是原地进行的（in place），会改变原数组的元素顺序。

快速选择与快排的思路基本相同，但是快速选择算法每次分治后，只处理一个子问题，而快排需要处理两个。那两者的复杂度有区别吗？

最坏情况复杂度：选择最小的元素，但是每次挑选主元都选了最大的，递归表达式如下：

$$
T(n)=n+(n-1)+\cdots+1=\Theta(n^2)
$$

故最坏情况的复杂度为$\Theta(n^2)$。

最好情况复杂度：第一次挑选主元都选到了第$k$位的元素，等同于split()的复杂度$O(n)$。

平均情况复杂度：假设所有元素互异，排第$i$位的元素被选取为主元的概率为$1/n$，$k$小于$i$的概率为$(i-1)/n$，$k$大于$i$的概率为$(n-i)/n$，$k$等于$i$的概率为$1/n$。可以列出以下递归关系式：

$$
\begin{equation}
\begin{aligned}
T(n) & = \frac{1}{n}\sum_{i=1}^n [\frac{i-1}{n}T(i-1)+\frac{1}{n}O(1)+\frac{n-i}{n}T(n-i)+O(n)] \\ & = \frac{1}{n^2}\sum_{i=1}^n[(i-1)T(i-1)+(n-i)T(n-i)]+O(n)
\end{aligned}
\end{equation}
$$

则：

$$
T(n-1)=\frac{1}{(n-1)^2}\sum_{i=1}^{n-1}[(i-1)T(i-1)+(n-1-i)T(n-1-i)]+O(n-1)
$$

联合两个式子，得：

$$
\begin{equation}
\begin{aligned}
T(n) & = \frac{(n+1)(n-1)}{n^2}T(n-1)+O(1) \\ &= O(1)[1+\frac{(n+1)(n-1)}{n\cdot n}+\frac{(n+1)(n-2)}{n(n-1)}+\frac{(n+1)(n-3)}{n(n-2)}+\cdots] \\ &= O(1)[1+\frac{n+1}{n}(n-\sum_{i=1}^n \frac{1}{i})] \\ &= O(n)
\end{aligned}
\end{equation}
$$

若存在相同元素，花费的时间显然小于$O(n)$，故平均复杂度为$O(n)$。

因此，利用分治策略，我们可以在$O(n)$时间内选出数组中排第$k$的元素。较常见的应用是寻找一个数组的中位数，只需要把快速选择算法的$k$设置为$(n+1)/2$。

Quick Link: 算法笔记整理

Like this article? Support the author with

Follow

Catalogue

Categories

Tags

Algorithms-Notes15
C++1
Cryptography1
Database1
Divide and Conquer1
FFT1
Hashing1
Internet1
Interview4
Number Theory6
Sorting1
Statistics1
Web APP1
iOS APP2
×