chap 2-1 分治算法-乘法、矩阵乘、主定理

1. 分治（Divide and Conquer）

分治算法是算法的重要分支之一，主要思想就是：

1. 自上而下把问题划分成几个小的子问题，每个子问题与原问题类型相同。
2. 自下而上递归地解决子问题。
3. 把子问题的解适当地组合成原问题的解。

虽然分治法的核心结构是递归，但也不一定非得用函数递归来实现；递归法便于分析问题，迭代法可能却更为高效 。

2. 乘法

假设$x$和$y$是两个$n-bit$整数（若不足$n$位则补零至$n$），为了使用分治法实现乘法，我们可以考虑将$x,y$各分成两半：

$$
x=(x_L)(x_R)=x_L\cdot 2^{\lfloor n/2 \rfloor}+x_R
$$

$$
y=(y_L)(y_R)=y_L\cdot 2^{\lfloor n/2 \rfloor}+y_R
$$

其中，$x_L$为$x$靠左的$\lceil n/2 \rceil-bit$整数，$x_R$为$x$靠右的$\lfloor n/2 \rfloor-bit$整数；$y_L$为$y$靠左的$\lceil n/2 \rceil-bit$整数，$y_R$为$y$靠右的$\lfloor n/2 \rfloor-bit$整数。两者相乘：

$$
xy=(x_L\cdot 2^{\lfloor n/2 \rfloor}+x_R)(y_L\cdot 2^{\lfloor n/2 \rfloor}+y_R)=x_Ly_L\cdot 2^{2\lfloor n/2\rfloor}+(x_Ly_R+x_Ry_L)\cdot 2^{\lfloor n/2 \rfloor}+x_Ry_R
$$

观察发现，我们把大的问题$xy$分成了四个小的子问题$x_Ly_L,x_Ly_R,x_Ry_L,x_Ry_R$，可以写出如下的递归关系式：

$$
T(n)=4T(\lceil \frac{n}{2} \rceil)+O(n)
$$

根据推导（后面会证明），该算法复杂度为$O(n^2)$，与普通乘法并无二异。

再仔细想想，上述表达式中的$x_Ly_R+x_Ry_L$可以被写成$(x_L+x_R)(y_L+y_R)-x_Ly_L-x_Ry_R$。总的来看，子问题的数目就从4降到了3，这是否能降低复杂度？写出递归表达式：

$$
T(n)\leq3T(\lceil \frac{n}{2} \rceil+1)+O(n)
$$

容易看出，表达式内加上的常数项（$x_L+x_R,y_L+y_R$可能有$\lceil \frac{n}{2} \rceil+1$位）并不会影响最终的复杂度，我们不如写成：

$$
T(n)=3T(\lceil \frac{n}{2} \rceil)+O(n)
$$

根据推导，现在的复杂度为$O(n^{\log_2 3})\approx O(n^{1.59})$，比普通乘法要更快！

伪代码：

function multiply2(x, y){
	n = max(size of x, size of y)
	if n=1: return xy
	
	x_L, x_R = leftmost ⌈n/2⌉, rightmost ⌊n/2⌋ bits of x
	y_L, y_R = leftmost ⌈n/2⌉, rightmost ⌊n/2⌋ bits of y
	
	P1 = multiply2(x_L, y_L)
	P2 = multiply2(x_R, y_R)
	P3 = multiply2(x_L+x_R, y_L+y_R)
	return P1×2^(2⌊n/2⌋) + (P3-P1-P2)×2^(⌊n/2⌋) + P2
}

上述代码中，我们一直递归到了n=1的情况。在实际操作中，大整数被拆成的每个部分可能是16位，我们可以只递归到n=16的情况，然后直接用处理器内置的算术运算指令进行运算。

我们已经把乘法的复杂度从$O(n^2)$优化到了$O(n^{1.59})$，还有没有更快的方法呢？确实有，后面会提到。

3. 矩阵乘法

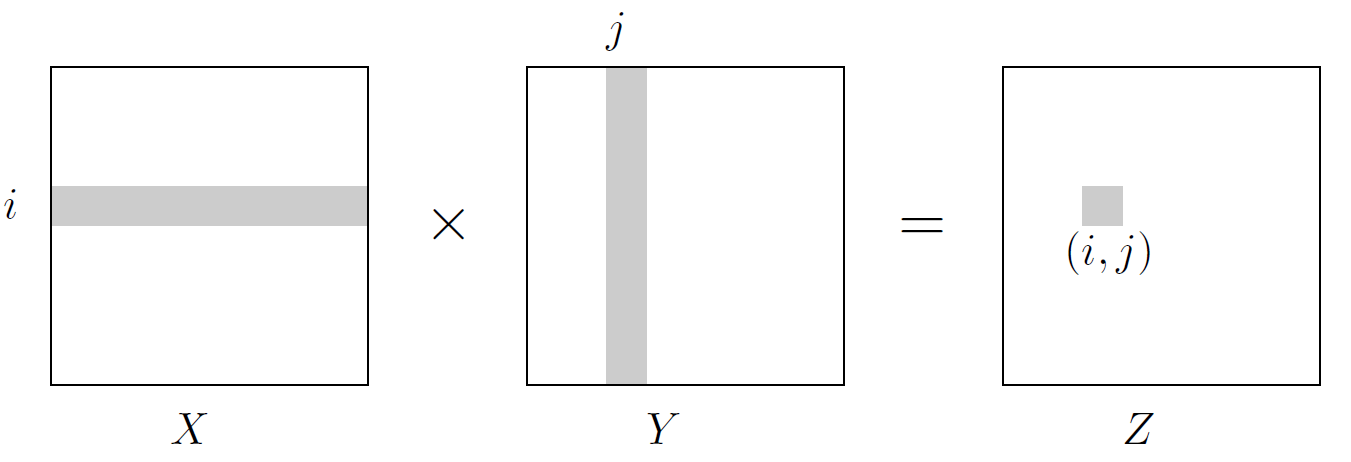
设$X,Y$都是$n\times n$的矩阵，$Z$为$X,Y$的乘积：

$$
Z_{ij}=\sum_{k=1}^n X_{ik}Y_{kj}
$$

使用以上表达式求解矩阵乘，复杂度为$O(n^3)$，有无更快的方法？

Strassen提出了一种基于分治法的矩阵乘算法。$X,Y$可以分别被划分成$\lceil n/2\rceil \times \lceil n/2\rceil$的四个块（block），若$n$不是偶数，则填补全零的一行/列：

$$
\begin{equation}
X=
\begin{bmatrix}
A & B \\ C & D
\end{bmatrix}
\end{equation}
$$

$$
\begin{equation}
Y=
\begin{bmatrix}
E & F \\ G & H
\end{bmatrix}
\end{equation}
$$

容易证明出：

$$
\begin{equation}
XY=
\begin{bmatrix}
A & B \\ C & D
\end{bmatrix}
\begin{bmatrix}
E & F \\ G & H
\end{bmatrix}
=\begin{bmatrix}
AE+BG & AF+BH \\ CE+DG & CF+DH
\end{bmatrix}
\end{equation}
$$

算出结果后要删除掉之前填补过的全零行/列。

上述算法把求解$XY$的问题，分成了8个子问题，可以列出下面的递归关系式：

$$
T(n)=8T(\lceil \frac{n}{2}\rceil)+O(n^2)
$$

根据推导，复杂度为$O(n^3)$。Strassen所做的优化与上面的乘法优化一样，把8个子问题缩减到了7个子问题：

$$
P_1=A(F-H)
$$

$$
P_2=(A+B)H
$$

$$
P_3=(C+D)E
$$

$$
P_4=D(G-E)
$$

$$
P_5=(A+D)(E+H)
$$

$$
P_6=(B-D)(G+H)
$$

$$
P_7=(A-C)(E+F)
$$

$$
\begin{equation}
XY=

=\begin{bmatrix}
P_5+P_4-P_2+P_6 & P_1+P_2 \\ P_3+P_4 & P_1+P_5-P_3-P_7
\end{bmatrix}
\end{equation}
$$

此时递归关系式变为：

$$
T(n)=7T(\lceil \frac{n}{2}\rceil)+O(n^2)
$$

根据推导，Strassen矩阵乘算法的复杂度为$O(n^{\log_2 7})\approx O(n^{2.81})$。

4. 主定理（Master Theorem）

分析分治算法的复杂度时，我们都推出了递归关系式，如何快速根据关系式得到复杂度呢？可以直接使用主定理：

Master Theorem

令 $a\geq 1$和 $b>1$是常数，$f(n)$是一个函数，$T(n)$是定义在非负整数上的递归表达式：

$$
T(n)=aT(n/b)+f(n)
$$

其中，$n/b$可以是 $\lceil n/b \rceil$或是 $\lfloor n/b \rfloor$，那么 $T(n)$有如下渐进界：

1. 若对于某个常数 $\varepsilon>0$有 $f(n)=O(n^{\log_b a -\varepsilon})$，则 $T(n)=\Theta(n^{\log_b a})$。
2. 若 $f(n)=\Theta(n^{\log_b a})$，则 $T(n)=\Theta(n^{\log_b a}\log n)$。
3. 若对于某个常数 $\varepsilon>0$有 $f(n)=\Omega(n^{\log_b a +\varepsilon})$，且对于某个常数 $c<1$和所有足够大的 $n$有 $af(n/b)\leq cf(n)$，则 $T(n)=\Theta(f(n))$。

简单来说就是，我们将函数$f(n)$与$n^{\log_b a}$进行比较：若$f(n)$渐进小于（多项式意义上小于，小$n^{\varepsilon}$这么多）$n^{\log_b a}$，则$T(n)=\Theta(n^{\log_b a})$；若$f(n)$渐进等于$n^{\log_b a}$，则$T(n)=\Theta(n^{\log_b a}\log n)$；若$f(n)$渐进大于$n^{\log_b a}$（多项式意义上大于，大$n^{\varepsilon}$这么多），且满足正则条件$af(n/b)\leq cf(n)$（大多数多项式界函数都满足），则$T(n)=\Theta(f(n))$。

不是所有情况都能直接套用主定理，比如$T(n)=2T(n/2)+n\log n$就无法套用情况3。

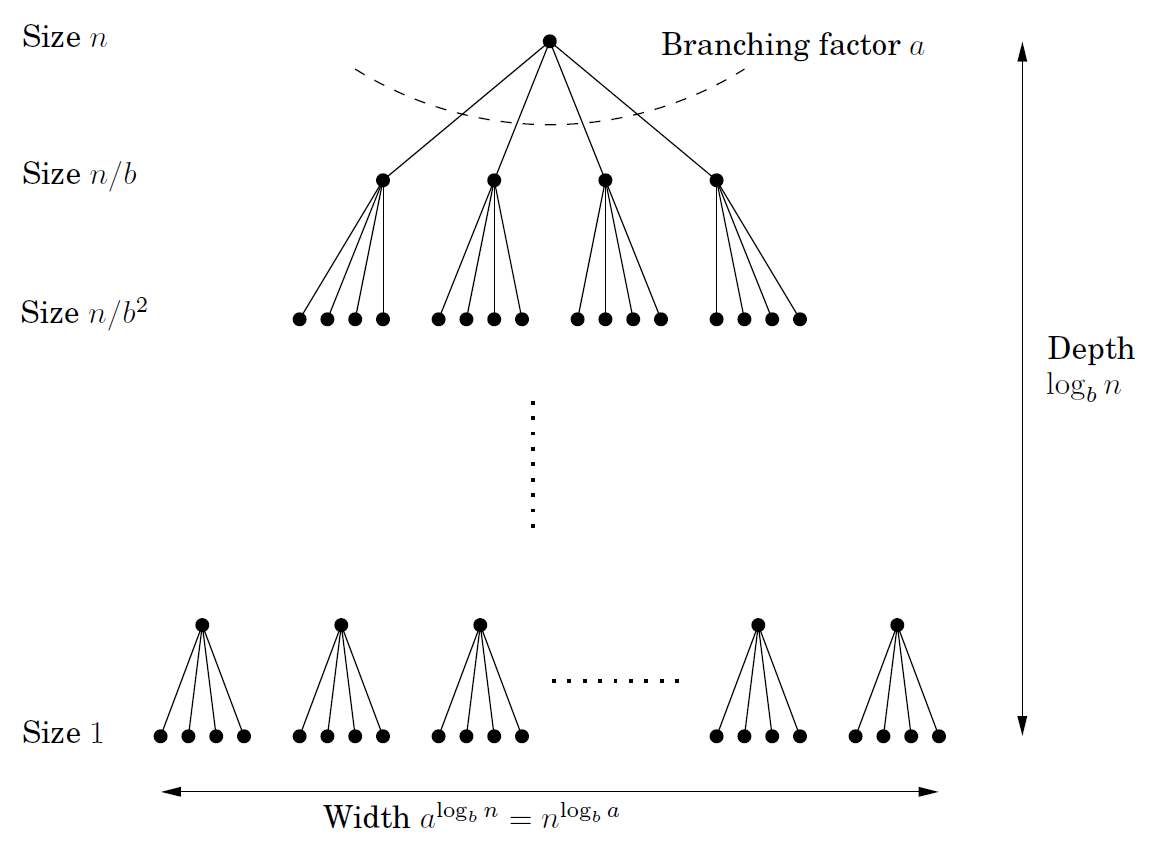
$Proof$：首先证明若$n$恰好为$b$的幂的情况。

根据递归树，容易推出：

$$
\begin{equation}
\begin{aligned}
T(n) & = aT(n/b)+f(n) \\ & =a^2T(n/b^2)+f(n)+af(n/b) \\ &= a^3f(n/b^3)+f(n)+af(n/b)+a^2f(n/b^2) \\ &= \cdots \\ &=a^{\log_b n}\cdot\Theta(1)+\sum_{k=0}^{\log_b n - 1} a^kf(n/b^k) \\ &=\Theta(n^{\log_b a})+\sum_{k=0}^{\log_b n - 1} a^kf(n/b^k)
\end{aligned}
\end{equation}
$$

令$g(n)=\sum_{k=0}^{\log_b n - 1} a^kf(n/b^k)$，

对于情况1：$f(n)=O(n^{\log_b a -\varepsilon})$，代入公式：

$$
\begin{equation}
\begin{aligned}
g(n) &=O(\sum_{k=0}^{\log_b n - 1} a^k(\frac{n}{b^k})^{\log_b a -\varepsilon}) \\ &=O(n^{\log_b a -\varepsilon}\sum_{k=0}^{\log_b n - 1}(b^{\varepsilon})^k) \\ &= O(n^{\log_b a -\varepsilon}\cdot\frac{n^{\varepsilon}-1}{b^{\varepsilon}-1}) \\ &= n^{\log_b a -\varepsilon}\cdot O(n^{\varepsilon}) \\ &=O(n^{\log_b a})
\end{aligned}
\end{equation}
$$

带入$T(n)$的表达式，可得$T(n)=\Theta(n^{\log_b a})$。

对于情况2：$f(n)=\Theta(n^{\log_b a})$，代入公式：

$$
\begin{equation}
\begin{aligned}
g(n) &=\Theta(\sum_{k=0}^{\log_b n - 1} a^k(\frac{n}{b^k})^{\log_b a}) \\ &= \Theta(n^{\log_b a}\cdot \sum_{k=0}^{\log_b n - 1}1 ) \\ &=\Theta(n^{\log_b a}\log n)
\end{aligned}
\end{equation}
$$

带入$T(n)$的表达式，可得$T(n)=\Theta(n^{\log_b a}\log n)$。

对于情况3：首先证明一下，对于某个常数 $c<1$和所有足够大的$n$有$af(n/b)\leq cf(n)$，就已经暗含了若对于某个常数$\varepsilon>0$有$f(n)=\Omega(n^{\log_b a +\varepsilon})$。将$af(n/b)\leq cf(n)$迭代$k$次，可得$a^kf(n/b^k)\leq c^kf(n)$，令$n=b^k$，则$f(n)\geq (a/c)^{\log_b n}\cdot f(1)=n^{\log_b a - \log_b c}\cdot f(1)$，即$f(n)=\Omega(n^{\log_b a +\varepsilon})$。

观察$g(n)$的表达式，可知$g(n)=\Omega(f(n))$。又因为：

$$
\begin{equation}
\begin{aligned}
g(n) &=\sum_{k=0}^{\log_b n - 1} a^kf(n/b^k) \\ &\leq \sum_{k=0}^{\log_b n - 1} c^kf(n)+O(1) \\ &\leq f(n) \sum_{k=0}^{\infty} c^k+O(1) \\ &= f(n)\cdot\frac{1}{1-c}+O(1)\\ &=O(f(n))
\end{aligned}
\end{equation}
$$

故$g(n)=\Theta(f(n))$。带入$T(n)$的表达式，可得$T(n)=\Theta(f(n))$。

下面证明若$n$不是$b$的幂的情况。易证有如下不等式成立：

$$
\cdots\leq n/b\leq b^{\lfloor \log_b n\rfloor-1}\leq n\leq b^{\lfloor \log_b n\rfloor}\leq bn\leq b^{\lfloor \log_b n\rfloor+1}\leq\cdots
$$

上述不等式说明，对于任意$n$，都能在附近找到一个比它大的数（不大于$bn$）使其称为$b$的幂，都能在附近找到一个比它小的数（不小于$n/b$）使其称为$b$的幂。

先考虑上取整的情况，参数调用序列如下：

$$
n,\lceil n/b \rceil,\lceil \lceil n/b \rceil/b \rceil,\lceil \lceil \lceil n/b \rceil/b \rceil/b \rceil,\cdots
$$

令$n_k$表示序列中的第$k$个元素：

$$
\begin{equation}
n_k=
\begin{cases}
n, & k=0 \\ \lceil n_{k-1}/b \rceil, & k>0
\end{cases}
\end{equation}
$$

则根据上述不等式，可得$n_k\in[b^{\lfloor \log_b n\rfloor-1}/b^k,b^{\lfloor \log_b n\rfloor}/b^k]$，即$n_k=\Theta(n/b^k)$。

根据递归树，容易推出：

$$
T(n)=\Theta(n^{\log_b a})+\sum_{k=0}^{\lfloor\log_b n\rfloor - 1} a^kf(n_k)
$$

令$g(n)=\sum_{k=0}^{\lfloor\log_b n\rfloor - 1} a^kf(n_k)$，

对于情况1：$f(n)=O(n^{\log_b a -\varepsilon})$，代入公式：

$$
\begin{equation}
\begin{aligned}
g(n) &=\sum_{k=0}^{\lfloor\log_b n\rfloor - 1} a^kO(n_k^{\log_b a -\varepsilon}) \\ &= O(\sum_{k=0}^{\lfloor\log_b n\rfloor - 1} a^k(\frac{n}{b^k})^{\log_b a -\varepsilon}))
\end{aligned}
\end{equation}
$$

证明同上。

对于情况2：$f(n)=\Theta(n^{\log_b a})$，代入公式：

$$
\begin{equation}
\begin{aligned}
g(n) &=\sum_{k=0}^{\lfloor\log_b n\rfloor - 1} a^k\Theta(n_k^{\log_b a}) \\ &= \Theta(\sum_{k=0}^{\lfloor\log_b n\rfloor - 1} a^k(\frac{n}{b^k})^{\log_b a})
\end{aligned}
\end{equation}
$$

证明同上。

对于情况3：观察$g(n)$的表达式，可知$g(n)=\Omega(f(n))$。根据$af(n_1)\leq cf(n)$，容易推出$a_kf(n_k)\leq c^k f(n)$，证明同上。

下取整的证明与上取整几乎相同，此处不再赘述。▮

现在忘了上面繁琐的证明吧，直接记住下面简化版本的主定理，已经能解决大部分问题了：

Master Theorem (simplified)

令 $a\geq 1$和 $b>1$是常数，$T(n)$是定义在非负整数上的递归表达式：

$$
T(n)=aT(n/b)+O(n^d)
$$

其中，$n/b$可以是 $\lceil n/b \rceil$或是 $\lfloor n/b \rfloor$，那么 $T(n)$有如下渐进界：

$$
\begin{equation}
T(n)=
\begin{cases}
O(n^{\log_b a}), & \log_b a>d \\ O(n^d\log n), & \log_b a=d \\ O(n^d), & \log_b a<d
\end{cases}
\end{equation}
$$

使用简化版的主定理，可以一眼看出上述提到的乘法和矩阵乘的复杂度：

$$
T(n)=3T(\frac{n}{2})+O(n),\log_b a=\log_2 3 > d=1,O(n^{\log_23})
$$

$$
T(n)=7T(\frac{n}{2})+O(n^2),\log_ba=\log_27>d=2,O(n^{\log_27})
$$

Quick Link: 算法笔记整理