chap 1-7 数论算法-全域哈希
1. 哈希表
数论算法在哈希函数的设计方面也有应用。假设在编写网络服务应用时,我们需要维护一个动态变化的客户的IPv4地址的list,如何快速地查询某个IP呢?一个最快的方法是建立大小为$2^{32}$的array,以IP作为index。虽然很快,但是会非常浪费内存,大多数内存可能都是空的。还有一个方法是使用链表,但是查询速度很慢,与客户个数成正比。使用哈希的方法能使占用内存的大小与客户数量成正比,同时获得较快的查询速度。
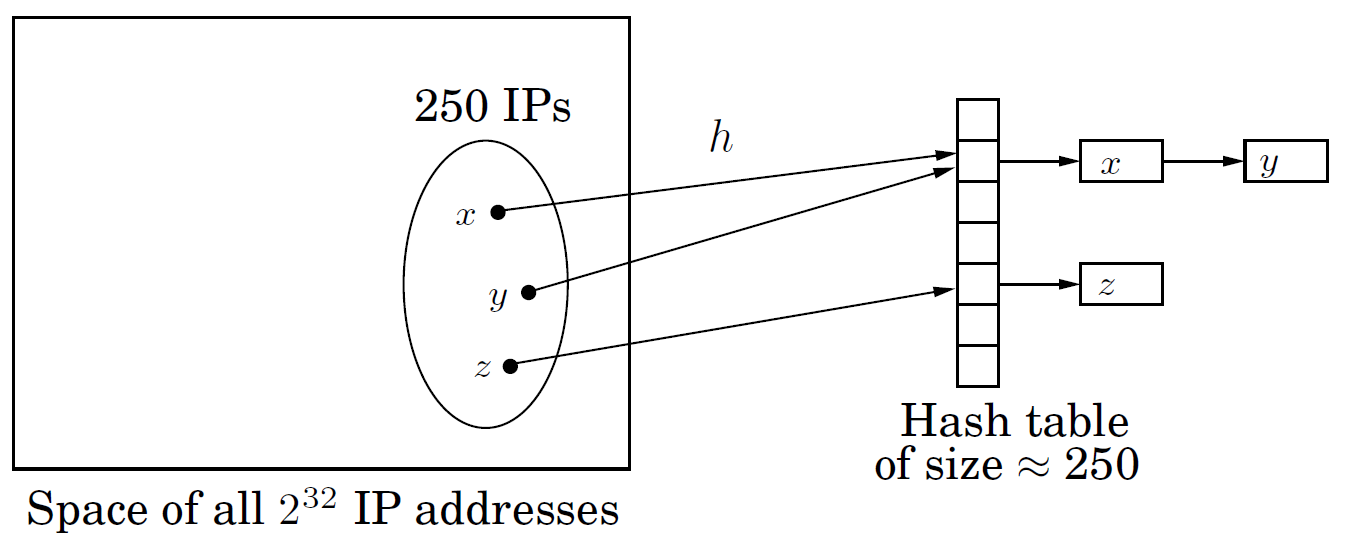
最常用的结构是Hash Table。假设现在有250个客户IP,我们可以建立一个大小为250的array作为哈希表。定义一个哈希函数$h(x)$,输入为客户的IP,输出为array的index值,该IP的具体信息存储在array[index]中。如果多个IP映射到同一个index怎么办(即碰撞)?那就把array每个元素改造成一个链表,同时存储多个IP,即每个元素都是一个bucket,里面装着若干个IP。故该算法的效率在最差的情况下,取决于一个bucket里面装了多少个IP。而IP映射到哪个bucket,是由哈希函数$h(x)$决定的。所以我们希望$h(x)$满足:无论$x$服从哪种概率分布,任意两个$h(x)$碰撞的概率都相等,即每个bucket里面装的IP都一样多。
不幸的是,如果我们只使用固定的一个$h(x)$,就不可能达到上述理想的效果,因为我们总能根据已知的若干$x$构造出一个$h(x)$使它们都被映射到同一个bucket中。
2. 哈希函数族
办法总比困难多,我们可以使用随机来中和掉输入分布的影响,那就是定义一组哈希函数,每次运行应用时,随机选用一个哈希函数,希望在平均意义上能达到理想效果。我们还是以IP为例,假设每个IP地址可以表示为$x=(x_1,x_2,x_3,x_4)$,$x_i$为0~255范围上的整数;假设有250个客户IP,令$n$为稍大于客户IP总数的一个素数,作为哈希表中bucket的数量。我们可以定义如下的哈希函数:
$$
h_a(x_1,x_2,x_3,x_4)=\sum_{i=1}^4 a_ix_i\mod n
$$
其中,$a_i\in$ {$0,1,\cdots, n-1$}。若每次随机挑选一组$a=(a_1,a_2,a_3,a_4)$组成哈希函数,那么在平均意义上,任意两个$x$冲突的概率为$\frac{1}{n}$:
假设$n$为素数,有整数 $x$,把$x$表示为 $x=(x_1,x_2,\cdots,x_k)$,使 $x_i\in$ { $0,1,\cdots, n-1$ };同理,$y$($y\neq x$)也可以被表示为 $y=(y_1,y_2,\cdots,y_k)$,使 $y_i\in$ { $0,1,\cdots, n-1$ };若系数为 $a=(a_1,a_2,\cdots,a_k)$,且每个 $a_i$都是从 { $0,1,\cdots, n-1$ } 中等概率随机选取的,那么:
$$
Pr[h_a(x_1,x_2,\cdots,x_k)=h_a(y_1,y_2,\cdots,y_k)]=\frac{1}{n}
$$
$Proof$:$h_a(x_1,x_2,\cdots,x_k)=h_a(y_1,y_2,\cdots,y_k)$等价于$\sum_{i=1}^k a_ix_i\equiv \sum_{i=1}^k a_iy_i (\mod n)$,即:
$$
\sum_{i=1}^{k-1} a_i(x_i-y_i)\equiv a_k(y_k-x_k) (\mod n)
$$
上述等式何时成立?假设我们已经随机选取了$a_{1:k-1}$的值,那么等式左边的值$c=\sum_{i=1}^{k-1} a_i(x_i-y_i)$就已经固定,所以只需要$a_k=c\cdot (y_k-x_k)^{-1}\mod n$,等式就会成立($c$和$y_k-x_k$必与$n$互质,$c$可以被约掉,$y_k-x_k$的乘法逆元也一定存在)。由于$a_k$是随机选取的,所以$a_k$恰好为$c\cdot (y_k-x_k)^{-1}\mod n$的概率为$\frac{1}{n}$,此时等式成立。故等式成立的概率为$\frac{1}{n}$。▮
综上,我们证明出了,使用随机选取的$h_a$,任意两个输入冲突的平均概率为$\frac{1}{n}$;换句话说,设所有可能取到的$h_a$的总数为$|H|$,那么有$|H|/n$个$h_a$能把不同的$x$映射到同一个bucket。
现在假设有$m$个不同的数需要被填到哈希表中,$n$为略大于$m$的素数;假设随机变量$Y_i$($1\leq i \leq m$)表示第$i$个数是否与固定的一个数$x$冲突,冲突则等于1,不冲突则等于0;根据上面的结论,可以得到:$E[Y]=\frac{1}{n}$。显然,$Y=Y_1+Y_2+\cdots+Y_m$表示所有与$x$冲突的数的个数,则$E[Y]=E[Y_1+Y_2+\cdots+Y_m]=\frac{m}{n}$。所以,使用这个方法,能够在平均意义上,使 “$h(x)$满足:无论$x$服从哪种概率分布,任意两个$h(x)$碰撞的概率都相等,即每个bucket里面装的IP都一样多。”
一组哈希函数$h(x)$,被称为一个哈希函数族$H$。若该哈希函数族满足:
对于任意两个不同的输入 $x$和 $y$,恰好有 $|H|/n$个哈希函数把 $x$和 $y$映射到同一个bucket中($n$为bucket的数量),则称这个哈希函数族具有全域哈希性(universal)。
换句话说,全域哈希性表明,对于任意两个输入,如果从函数族里随机选取一个哈希函数做映射,那么在平均意义上讲(in expectation),它们冲突的概率为$\frac{1}{n}$。这就等价于把$x$和$y$随机放入bucket中。总结就是:全域哈希插入、查询的平均性能较好。
在应用中使用全域哈希的步骤:
- 把输入$x$分割成$k$个部分,令$n$为稍大于每个部分最大值的素数。
- 全域哈希函数族为:$H=$ {$h_a:a\in$ {$0,1,\cdots,n-1$}$^k$}。
- 从上述函数族中随机选取一个$h_a$作为哈希函数。
Quick Link: 算法笔记整理