chap 1-6 数论算法-密码学

1. 密码学简介

数论算法应用最广泛的领域之一就是密码学，密码学也是网络安全的重要研究分支。密码学研究的主要问题可以用以下情境描述：Alice和Bob二人想要进行私密通信，但是Eve想要偷听他们的私密通信。Alice和Bob为了保证私密性，他们决定对消息进行加密和解密（编码和译码）：

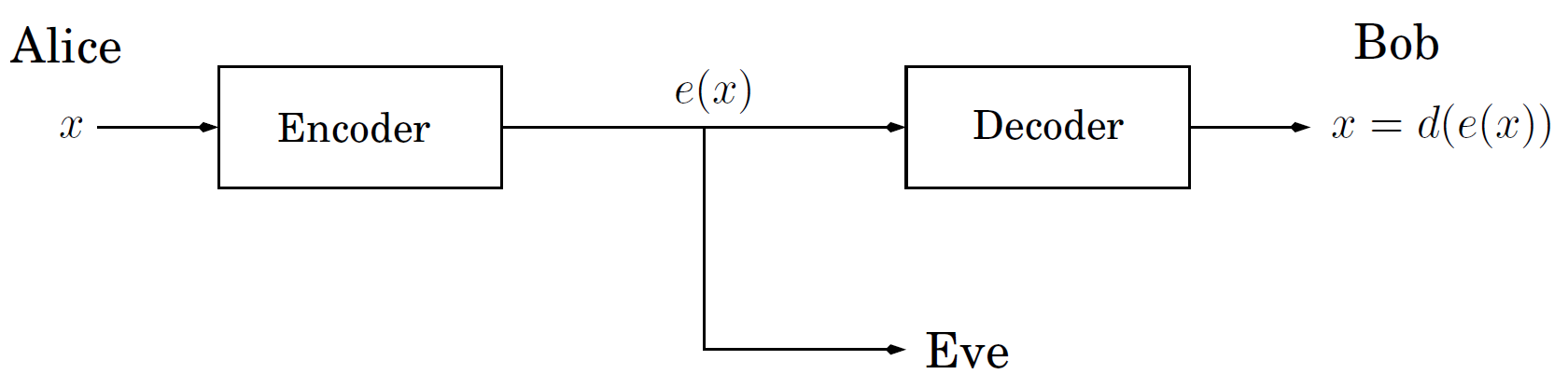
Alice把消息$x$编码为$e(x)$，然后发送消息；Eve可以在半路中截获$e(x)$；Bob收到加密消息$e(x)$后，使用解密函数$d(\cdot)$译码，即$d(e(x))=x$。最理想的效果是，只要不知道$d(\cdot)$就无法破解出$x$。

密码学主要分为两个体系：私钥（private-key）体系和公钥（public-key）体系。

私钥的主要思想是：Alice和Bob提前确定好一个密码本（codebook），加密和解密都根据密码本上面（原文，译文）一对一的关系进行。这里的密码本就是私钥。

公钥的主要思想是：Bob把自己的公钥公布于众，自己保留一个secret-key。Alice利用公钥加密消息发给Bob。Bob利用secret-key可以轻松地解密，Eve由于不知道secret-key，在某些条件成立的情况下基本不可能解密。

2. 一次性密钥与AES算法

一次性密钥（one-time pad）和AES（Advanced Encryption Standard）算法都是私钥体系的典型代表。

在一次性密钥算法中，Alice和Bob提前商量好了一个$n-bit$二进制串$r$，Alice加密消息时使用下面的函数：

$$
e_r(x)=x\oplus r
$$

$\oplus$为异或操作，假设$r=01110010$，则$e_r(11110000)=11110000\oplus 01110010=10000010$。

Bob收到加密消息$y$时，使用如下的函数解密：

$$
d_r(e_r(x))=e_r(x)\oplus r= (x\oplus r)\oplus r=x\oplus (r \oplus r)=x\oplus 0=x
$$

如何选取$r$？每次传输消息的时候，随机选取就行，这就保证了Eve截获了$e_r(x)$后无法判断$x$的值，因为$x$可能是任何值。

每传一次消息，需要换一次$r$吗？确实需要，这也是一次性密钥算法的缺点。如果Eve知道了每次的$r$不会变，他就可以截获多个$e_r(x)$，推断出$x$的一些特性；若截获的数量很多，甚至可以直接推出$r$的值。因此，一次性密钥算法要求Alice和Bob再每次传输消息前，都要事先协商好$r$的值。

AES算法可以说是“永久性”密钥算法。AES使用了一个128位（也有其他位数）的私钥$r$，Alice和Bob之前需要协商好。与一次性密钥不同的是，AES使用的加密函数利用$r$（消息可以被截断成多个128位的片段），对每个消息片段进行了多次变换，很难通过截获的$e(x)$获取任何关于$x$和$r$的信息，故私钥$r$可以被重复使用。至少在目前，除了一个个试$r$的值，还没有找到合适的破解方法。

代码实现（一次性密钥）：

int naive_AES_encode(int x, int r) {
	return x ^ r;
}

int naive_AES_decode(int y, int r) {
	return y ^ r;
}

3. RSA算法

RSA算法与上面的算法不同，它属于公钥体系。RSA的原理使用了非常多数论的知识，前几章提到的各种算法现在终于能大展身手了！

假设Alice发给Bob的消息是一个数字$x\mod N$后的值（$x$大于$N$就把消息分割成小片段，使其小于$N$），随机选取两个素数$p$和$q$，令$N=pq$，令$e$为任意与$(p-1)(q-1)$互质的一个数，那么有以下性质成立：

1. $x\to x^e\mod N$的映射关系是在集合{ $0,1,\cdots, N-1$ }上的双射（一一对应）。
2. 逆映射：令 $d$为 $e\mod (p-1)(q-1)$的乘法逆元，则 $(x^e)^d\equiv x (\mod N)$。

$Proof$：先证明第二个性质。$d$为 $e\mod (p-1)(q-1)$的乘法逆元，即$ed\equiv 1 (\mod (p-1)(q-1))$，可以把$ed$表示为$1+k(p-1)(q-1)$。根据费马小定理：$x^{p-1}\equiv 1 (\mod p)$成立，而$p$能整除$N$，可以推出：$x^{p-1}\equiv 1 (\mod N)$；同理，$x^{q-1}\equiv 1 (\mod N)$。所以，$x^{ed}-x\equiv x^{1+k(p+1)(q+1)}-x\equiv x-x\equiv 0 (\mod N)$，即$(x^e)^d\equiv x (\mod N)$。第二个性质成立，说明映射可逆，证明了第一个性质也成立。▮

利用上述性质，设计出RSA加密算法：

1. Bob公布public-key，保留secret-key：
   • 选择两个大的$n-bit$随机素数$p$和$q$。
   • 公布public-key$(N,e)$，其中$N=pq$，$e$为任意$2n-bit$的与$(p-1)(q-1)$互质的数。通常选取$e=3$，算的会快一些。
   • 保留secret-key $d$，$d$为$e\mod (p-1)(q-1)$的乘法逆元。
2. Alice发送消息$x$给Bob：
   • 使用Bob公布的public-key$(N,e)$，发送$y=x^e\mod N$。
3. Bob使用secret-key $d$解密：
   • 计算出$y^d\mod N$。

现在邪恶的Eve想要破解出$x$。给定$N,x$，截获了$y=x^e\mod N$，有可能计算出$x$吗？两种方法：第一种是穷举$x$，判断$y=x^e\mod N$是否成立，但复杂度为指数级，$n-bit$很大时，无法算出。第二种是猜出$p$和$q$，从而获取$d$。但是，$N$为一个很大的数，对大数进行质因数分解非常困难，复杂度也是指数级，故也无法算出。

总结来说，RSA能够成为最常用的加密算法，基于的前提是：目前没有高效的质因数分解算法。

对比AES算法，RSA算法虽然安全性极高，但是开销同样很大。实际应用时，常常是先用RSA算法加密传输私钥，然后使用AES算法利用私钥通信，因为AES的开销要小得多。

RSA的代码实现：

pair<int, int> gen_public_key(int p, int q) {
	int N = p * q;
	int e = 3;
	return make_pair(N, e);
}

int gen_private_key(int e, int p, int q) {
	int d = get_multiplicative_inverse(e, (p - 1) * (q - 1));
	return d < 0 ? d + (p - 1) * (q - 1) : d;
}

// x < N
int naive_RSA_encode(int x, int N, int e) {
	return modexp(x, e, N);
}

int naive_RSA_decode(int y, int N, int d) {
	return modexp(y, d, N);
}

测试结果：

naive_RSA_test
Input an integer x as a message: 12345
Pick two large random primes: (10601, 19763)
Public key: (209507563, 3)
Private key: 139651467
Encoded: 197555448
Decoded: 12345
time = 29ms
======================================
naive_RSA_test
Input an integer x as a message: 73658734
Pick two large random primes: (10601, 19763)
Public key: (209507563, 3)
Private key: 139651467
Encoded: 183414919
Decoded: 73658734
time = 28ms
======================================

Quick Link: 算法笔记整理