chap 1-3 数论算法-模运算

1. 模运算

我们知道，计算机处理器进行内置的算术运算时，数字大小都是有限制的（32 bits or 64 bits），这已经可以满足绝大多数计算需求了。但如果不断地对一个数做加法或乘法运算，它将变得非常大，最终将会溢出(overflow)。如何解决这个问题？可以从日常生活中得到启发：日复一日，年复一年… 第二天又是新的24小时，第二年又是新的十二个月…

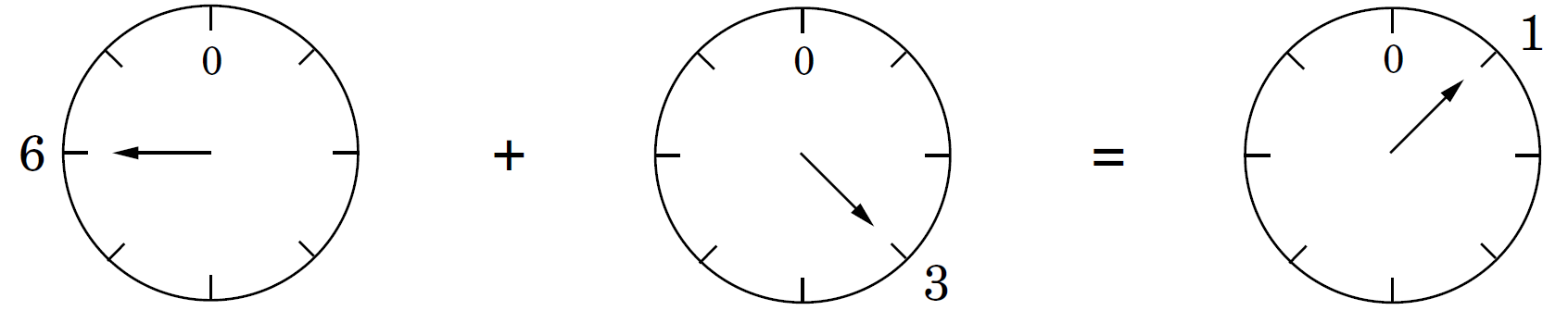
于是，为了把数字限制在一定的区间(range)内，模运算应运而生：

$x \mod N$表示 $x/N$ 的余数，即：若 $x=qN+r(0\leq r < N)$，则 $x\mod N=r$。

建立了新的模运算体系，有必要重新研究一下一些基本运算。

最重要的运算，判断两数是否相等：$1\neq 25$，但是 $1 \mod 24=25\mod 24$（一天24小时），在这种情况下1和25是等价的。于是我们定义模运算下的相等：

如果 $x$ 和 $y$ 的差值为 $N$ 的整数倍数，那么称 $x$和 $y$ 对模 $N$ 同余，即 $x\equiv y(\mod N)$ <=> $N整除x-y$。

$x$ 和 $y$ 对模 $N$ 同余的含义就是：$x\mod N = y\mod N$。

形象理解模运算：把数字限制在区间{$0,1,2,\cdots,N-1$}里，只要跃出区间，就再映射回去。

抽象理解模运算：把全体数字分成 $N$ 类，属于{$i+kN: k\in Z, 0\leq i\leq N-1$}区间中的数都被视为 $i$。

2. 模运算的性质

既然模运算的作用是限制数字大小，那么在计算的过程中是否可以先进行模运算，然后再做加减乘除？下面的几个基本性质为我们提供了便利。

代换律：若 $x\equiv x’(\mod N)$且 $y\equiv y’(\mod N)$，则 $x+y\equiv x’+y’(\mod N)$，$xy\equiv x’y’(\mod N)$

$Proof:$ $(x+y)-(x’-y’)=(x-x’)+(y-y’)$ 可被$N$整除；$xy-x’y’=x(y-y’)+y(x-x’)$ 可被 $N$ 整除。▮

结合律：$x+(y+z) \equiv (x+y)+z (\mod N)$

交换律：$xy \equiv yx (\mod N)$

分配律：$x(y+z) \equiv xy+yz (\mod N)$

若干推论：

$(x+y)\mod N=((x\mod N) + (y\mod N))\mod N$

$(x-y)\mod N=((x\mod N) - (y\mod N))\mod N$

$x\cdot y\mod N=((x\mod N)\cdot(y\mod N))\mod N$

$x^y\mod N=(x\mod N)^y\mod N$

上面的性质告诉我们：在做加、减、乘、乘方的带模的混合运算时，可以在任何阶段对数字取模 $N$ 来减小中间结果。

举例：$2^{345}\equiv 32^{69} \equiv 1^{69} \equiv 1 (\mod 31)$, $2^{2^{2006}}\equiv 4^{2^{2005}}\equiv 1^{2^{2005}}\equiv 1 (\mod 3)$。

还有一些常用的性质：

若 $a\equiv b (\mod N)$且$M$整除$N$，则 $a\equiv b(\mod M)$。

$Proof$：设$a-b=k_1N$，由于$M$整除$N$，设$N=k_2M$，故$a-b=(k_1k_2)M$，即$a\equiv b(\mod M)$。▮

若 $ac\equiv bc(\mod N)$且 $c,N$互质，则 $a\equiv b(\mod N)$。

$Proof$：$ac\equiv bc(\mod N)$等价于$(a-b)c\equiv 0(\mod N)$，表明$(a-b)c$整除$N$，由于$c,N$互质，所以$a-b$整除$N$，即$a\equiv b(\mod N)$。▮

3. + - × 的模运算

在模运算体系中计算 $x+y\mod N$ 的复杂度是多少？$x, y$一定在 $0$ 到 $N-1$ 的区间中，它们的和一定在 $0$ 到 $2(N-1)$ 的区间中。若和超过 $N-1$，则需将结果减去 $N$。总复杂度应该为 $O(n)$，其中 $n=\lceil \log N \rceil$。减法也是同理。

在模运算体系中计算 $xy\mod N$ 的复杂度是多少？$x, y$ 一定在 $0$ 到 $N-1$ 的区间中，它们的积一定在 $0$ 到 $(N-1)^2$ 的区间中，至多有 $2n$ bits（$\log (N-1)^2 \leq 2n$）。若积超过 $N-1$，则需将结果除以 $N$，获取余数。总复杂度应该为 $O(n^2)$，其中 $n=\lceil \log N \rceil$。

在模运算体系中如何计算除法结果？由于除法不具有加法和乘法的模运算性质，所以计算方法要复杂得多，后面再细讲。先提前透露一下复杂度，可以在 $O(n^3)$ 内完成。

4. 指数的模运算

除了基本的四则运算，幂运算同样会使数字增长到很大，模运算如何解决这个问题？

假设有正整数 $x$ 和 $y$，我们需要计算出 $x^y\mod N$。仿照 $n-bit$ 乘法的实现，我们可以写出以下递归表达式：

$$
\begin{equation}
x^y=
\begin{cases}
(x^{\lfloor\frac{y}{2}\rfloor})^2, & y为偶数 \\ x\cdot (x^{\lfloor\frac{y}{2}\rfloor})^2, & y为奇数
\end{cases}
\end{equation}
$$

根据模运算的性质，在这里对任何中间结果取模再运算，与最后真实的结果是同余的：

$$
x^y\equiv (x^{\lfloor\frac{y}{2}\rfloor}\mod N)\cdot (x^{\lfloor\frac{y}{2}\rfloor}\mod N) (\mod N)
$$

$$
x^y\equiv (x\mod N)\cdot(x^{\lfloor\frac{y}{2}\rfloor}\mod N)\cdot (x^{\lfloor\frac{y}{2}\rfloor}\mod N) (\mod N)
$$

故可以用以下代码实现带模的幂运算（快速幂）：

// N = 1337
int modexp(int x, int y, int N) {
	if (y == 0) return 1;
	int z = modexp(x, y / 2, N);
	if (y % 2 == 0) return (z * z) % N;
	else return (x * z * z) % N;
}

测试结果：

modexp_test (N = 1337)
Input integer x: 5
Input integer y: 3
Output: 125
time = 0ms
======================================
modexp_test (N = 1337)
Input integer x: 2
Input integer y: 64
Output: 408
time = 0ms
======================================
modexp_test (N = 1337)
Input integer x: 12345678
Input integer y: 87654321
Output: 911
time = 1ms
======================================

上述代码在 $N=1337$ 时结果正确。但是如果 $N$ 足够大，运行结果仍然可能溢出：z*z或x*z*z有可能超出int的范围，可以利用模运算的性质中的推论进行进一步优化。在实际应用中，这段代码已经可以满足绝大多数计算需求了。

优化如下：

// 乘法导致了modexp溢出，故这里使用快速乘取模，将结果进一步限制住
int modmul(int x, int y, int N) {
	if (y == 0) return 0;
	int yy = modmul(x % N, y / 2, N);
	if (y % 2 == 0) return (2 * (yy % N)) % N;
	else return (x % N + (2 * (yy % N)) % N) % N;
}

// N < (2^31 - 1) / 2
int modexp(int x, int y, int N) {
	if (y == 0) return 1;
	int z = modexp(x % N, y / 2, N);
	if (y % 2 == 0) return modmul(z, z, N);
	else return modmul(x % N, modexp(x % N, y - 1, N), N);
}

测试结果：

modexp_test (N = 1000000007)
Input integer x: 2
Input integer y: 1000
Output: 688423210
time = 1ms
======================================
modexp_test (N = 1000000007)
Input integer x: 100000001
Input integer y: 123456789
Output: 187658035
time = 68ms
======================================

下面分析一下算法复杂度，设 $n$ 为 $x, y, N$ 中最大数的位数，最多进行 $n$ 次递归调用，每次需要做 $n-bit$ 乘法，故总复杂度为 $O(n^3)$。

Quick Link: 算法笔记整理