chap 1-2 数论算法-乘除法

1. $n-bit$乘法的原理与实现

小学的时候就学过乘法的竖式计算，二进制乘法步骤如下：

              1 1 0 1    (13)
            × 1 0 1 1    (11)
------------------------
              1 1 0 1    (1101×1)
            1 1 0 1      (1101×1, shift left once)
          0 0 0 0        (1101×0, shift left twice)
      + 1 1 0 1          (1101×1, shift left thrice)
------------------------
      1 0 0 0 1 1 1 1    (143)

计算机硬件里乘法器的原理也是类似：

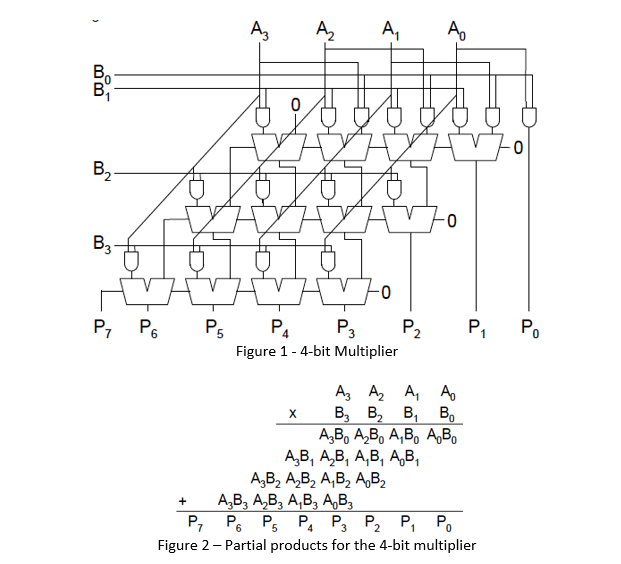
总结就是：$A$乘以$B$的第$k$位然后左移$k$位，作为部分积，最后累加所有部分积。这样做是否正确？

$Proof:$ 假设$N$和$M$是两个乘数，$M$为$k-bit$二进制整数，每一位为$b_k$，$M$可以被写做$M=b_0+2b_1+2^2b_2+\cdots +2^kb_k$。那么，$N\cdot M=Nb_0+2Nb_1+2^2Nb_2+\cdots +2^kNb_k$，这符合上述步骤的结果。

该算法的复杂度是多少？观察竖式，每生成一行部分积，复杂度为$O(n)$；最后要进行$n-1$次部分积求和，故总复杂度为$O(n^2)$。

换一种视角看待乘法，我们其实可以用递归的形式来表达上述步骤：

$$
\begin{equation}
x\cdot y=
\begin{cases}
2(x\cdot \lfloor\frac{y}{2}\rfloor), & y为偶数 \\ x+2(x\cdot \lfloor\frac{y}{2}\rfloor), & y为奇数
\end{cases}
\end{equation}
$$

$Proof:$ 若$y=2k$，则$2(x\cdot \lfloor\frac{y}{2}\rfloor)=2xk=xy$；若$y=2k+1$，则$x+2(x\cdot \lfloor\frac{y}{2}\rfloor)=x(2k+1)=xy$。▮

递归表达式中，除以2的操作就是右移，乘以2的操作就是左移。本质上与竖式计算相同，只不过竖式计算是自上而下累加部分积，这里是自下而上累加部分积。

利用递归形式，我们可以很容易写出伪代码：

function multiply(x, y){
    if(y = 0) return 0;
    z = multiply(x, y/2);
    if(y is even) return 2z;
    else return x + 2z;
}

具体实现：

Binary multiply(const Binary& x, const Binary& y) {
    if (y.is_zero()) return get_zero();
    Binary z = multiply(x, y.right_shift());
    if (y.is_even()) return z.left_shift();
    else return x + z.left_shift();
}

测试结果：

multiplication_test
Input the first binary integer a: 11
Decimal value of a: 3
Input the second binary integer b: 110
Decimal value of b: 6
Output: 10010
Decimal output: 18
time = 1ms
======================================
multiplication_test
Input the first binary integer a: 10101111101110
Decimal value of a: 11246
Input the second binary integer b: 101011
Decimal value of b: 43
Output: 1110110000011111010
Decimal output: 483578
time = 1ms
======================================

该递归算法的复杂度是多少？首先计算递归调用的次数，每次将$y$右移1位，所以总共调用$n$次，每次执行的复杂度为$O(n)$，故总复杂度仍然为$O(n^2)$。

是否存在更好的方法？确实存在，之后会详细介绍。

2. $n-bit$除法的原理与实现

假设$x/y$，除法的本质就是找到商$q$和余数$r$，使$x=qy+r$，其中$r<y$。

继续采用递归的形式实现算法：

假设$\lfloor \frac{x}{2}\rfloor / y = (q, r)$，$x=2k$且$2r<y$时，$x/y=(2q, 2r)$，若$2r\geq y$，则$x/y=(2q+1, 2r-y)$；

当$x=2k+1$且$2r+1<y$时，$x/y=(2q, 2r+1)$，若$2r+1\geq y$，则$x/y=(2q+1, 2r+1-y)$；

写成伪代码就是：

function divide(x, y){
    if(x == 0) return (q, r)=(0, 0);
    (q, r) = divide(x/2, y);
    q = 2q; 
    r = 2r;
    if(x is odd) r = r + 1;
    if(r >= y){
        r = r - y;
        q = q + 1;
    }
    return (q, r);
}

具体实现：

pair<Binary, Binary> divide(Binary& x, Binary& y) {
    if (x.is_zero()) return make_pair(get_zero(), get_zero());
    pair<Binary, Binary> res = divide(x.right_shift(), y);
    Binary q = res.first;
    Binary r = res.second;
    q = q.left_shift();
    r = r.left_shift();
    if (x.is_odd()) r = r + get_one();
    if (r > y || r == y) {
        r = r - y;
        q = q + get_one();
    }
    return make_pair(q, r);
}

算法的复杂度与乘法类似，都是$O(n^2)$。

Quick Link: 算法笔记整理