chap 1-1 数论算法-加减法

1. 浅谈基数(base)和$\log$

这章主要研究的对象是数字，首要的问题是，如何表示数字？众所周知，目前我们日常使用的都是十进制表示法（可能因为有十个手指头吧），计算机内部使用的都是二进制表示法。这里的“十”、“二”就是基数(base)。

假设现在用$b(b\geq 2)$-进制表示法。第一个问题，表示一个正整数$N\geq 0$需要至少多少位？我们知道，$k$位数字最大是$b^k-1$，那么可以推导出我们至少需要$\lceil \log_b (N+1) \rceil$位。

同一个数$N$分别用$b$-进制和$a$-进制表示，它们的位数有啥关系呢？推导一下：

$$
\lceil \log_a (N+1) \rceil=\lceil \log_b (N+1) \log_a b \rceil \leq \lceil \log_b (N+1) \rceil \lceil\log_a b \rceil
$$

可以得到一个有趣的推论：对于同一个数，用二进制法表示的位数最多是十进制法表示的位数的$\lceil\log_2 10 \rceil=4$倍。在实现大整数的进制转换时，可以利用这个推论提前分配空间。使用Big-$O$ Notation时，上述推论也同时说明了不管基数为多少，我们都可以直接使用$O(\log N)$来表示复杂度。

$O(\log N)$可以说是计算机学科的常客了，比如$N$节点完全二叉树的深度、二分法等等，都很容易想到$log N$。然而下面这个结论一眼看不出来：

$$
有限项调和级数：\sum_{i=1}^n \frac{1}{i}=\Theta(\log n)
$$

$Proof:$

$$
\begin{equation}
\begin{aligned}
\sum_{i=1}^n \frac{1}{i} & = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots \\ & \leq 1 + \frac{1}{2} + \frac{1}{2} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \cdots \\ &= 1 + 1 + 1 + \cdots \\ &= O(\log n)
\end{aligned}
\end{equation}
$$

$$
\begin{equation}
\begin{aligned}
\sum_{i=1}^n \frac{1}{i} & = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots \\ & \geq 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{4} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \cdots \\ &= 1 + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \cdots \\ &= O(\log n)
\end{aligned}
\end{equation}
$$

排序算法中，$O(N\log N)$也算是常客了。然而下面这个结论一眼也看不出来：

$$
\log(n!)=\Theta(n\log n)
$$

$Proof:$

$$
(\frac{n}{2})^{\frac{n}{2}} \leq n! \leq n^n
$$

$$
\frac{n}{2}\log \frac{n}{2} \leq log(n!) \leq n\log n
$$

$$
\frac{n}{2}\log n - \frac{n}{2} \leq log(n!) \leq n\log n
$$

有些扯远了，我们现在回到本章的主题。

2. 加法的性质

看到这，你可能觉得奇怪，加法不是小学起就学过，还能有啥性质呢？其实，加法竖式计算以及数字电路中加法器的设计就不知不觉使用了如下的性质：

假设一个整数，以 $b(b\geq 2)$作为基数(base)，即 $b$-进制。那么任意三个1位整数的和至多只会有2位。

举例：9+9+9=27, 001+001+001=011…

$Proof:$ 1位整数，最大值为$b-1$；任意三个1位整数之和最大值为$3b-3$；2位整数，最大值为$(b-1)\cdot b^1+(b-1)\cdot b^0=b^2-1$；由于$b^2-1-(3b-3)=(b-1)(b-2)\geq 0$，故上述性质成立。▮

有了这个性质，我们很容易就可以想到如何进行$b$-进制加法：将两个数右端对齐，从右至左依次对每一位求和，进位记为$carry$。性质表明，求和结果加上$carry$至多为2位，$carry$至多为1位。举例：

carry: 1 1 1 1
         1 1 0 1  (13)
       + 1 1 1 1  (15)
     -------------
       1 1 1 0 0  (28)

3. $n-bit$加法实现与分析

上述方法其实就是行波进位加法器的设计思想（参见数字电路设计），原理如下：

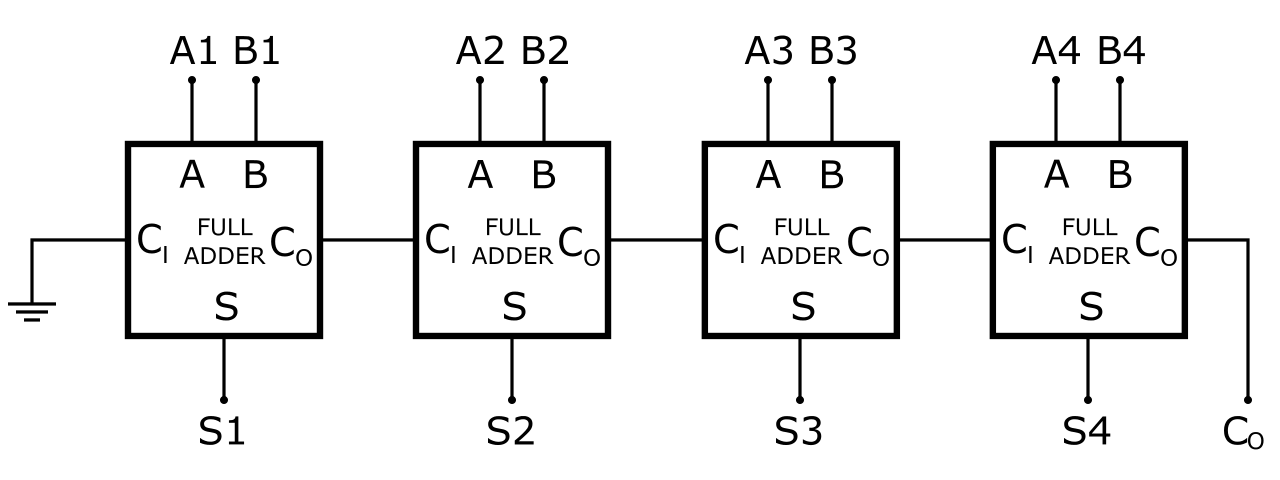
其中，$A_k$代表第1个加数的第$k$位的值，$B_k$代表第2个加数的第$k$位的值，$S_k$代表两数之和的第$k$位的值，$C$代表进位(carry)。

下面用代码模拟加法器的运行步骤，实现如下的二进制$n-bit$加法：

class Binary {
public:
	int* arr; // inverse order：0x1101 (13) => [1, 0, 1, 1], length=4
	int length;
	int MAX_LEN;
    
    Binary operator+(const Binary& num) {
		int* a = arr;
		int a_len = length;
		int* b = num.arr;
		int b_len = num.length;
		Binary addition = Binary();
		while (addition.MAX_LEN < max(a_len, b_len) + 2) addition.double_size();

		int* c = addition.arr;
		int carry = 0;
		int i;
		for (i = 0; i < max(a_len, b_len); ++i) {
			int res = (i<a_len?a[i]:0) + (i<b_len?b[i]:0) + carry;
			carry = 0;
			if (res > 1) {
				carry = 1;
				res -= 2;
			}
			c[i] = res;
		}
		if (carry == 1) {
			c[i] = 1;
			i++;
		}
		addition.length = i;
		return addition;
	}
}

再次考虑那三个问题，首先算法是否正确，下面为测试结果，没有明显错误：

addition_test
Input the first binary integer a: 1101
Decimal value of a: 13
Input the second binary integer b: 1111
Decimal value of b: 15
Output: 11100
Decimal output: 28
time = 1ms
======================================
addition_test
Input the first binary integer a: 111011
Decimal value of a: 59
Input the second binary integer b: 10
Decimal value of b: 2
Output: 111101
Decimal output: 61
time = 1ms
======================================
addition_test
Input the first binary integer a: 1010010101111010110
Decimal value of a: 338902
Input the second binary integer b: 1010111110111110101011
Decimal value of b: 2879403
Output: 1100010001101110000001
Decimal output: 3218305
time = 2ms
======================================

第二个问题，算法复杂度如何？显然是$O(n)$。

注意在本章中，我们考虑的算法复杂度都是细化到$bit$层级的，即复杂度是输入$n-bit$数字的$n$的函数。原因有二：首先，如果运算的数字变得非常大时（本章后面的算法），大数的运算原理和这里基本相同（可以了解一下Java中BigInteger的实现）；其次，有助于我们理解计算机的硬件是如何实现运算的。

第三个问题：是否有更快的算法？投机取巧一下，读取和输入都至少各要$n$次操作，所以$O(n)$已经是最优。

4. 减法

减法的原理和加法基本相同，不再赘述：

// Assume a>=b
Binary operator-(const Binary& num) {
    int* a = arr;
    int a_len = length;
    int* b = num.arr;
    int b_len = num.length;
    Binary subtraction = Binary();
    while (subtraction.MAX_LEN < max(a_len, b_len) + 2) subtraction.double_size();

    int* c = subtraction.arr;
    int carry = 0;
    int i;
    for (i = 0; i < max(a_len, b_len); ++i) {
        int minuend = i < a_len ? a[i] : 0;
        int subtrahend = (i < b_len ? b[i] : 0) + carry;
        carry = 0;
        if (minuend < subtrahend) {
            carry = 1;
            minuend += 2;
        }
        int res = minuend - subtrahend;
        c[i] = res;
    }
    while (i-1 > 0 && c[i-1] == 0) i--;
    subtraction.length = i;
    return subtraction;
}

Quick Link: 算法笔记整理